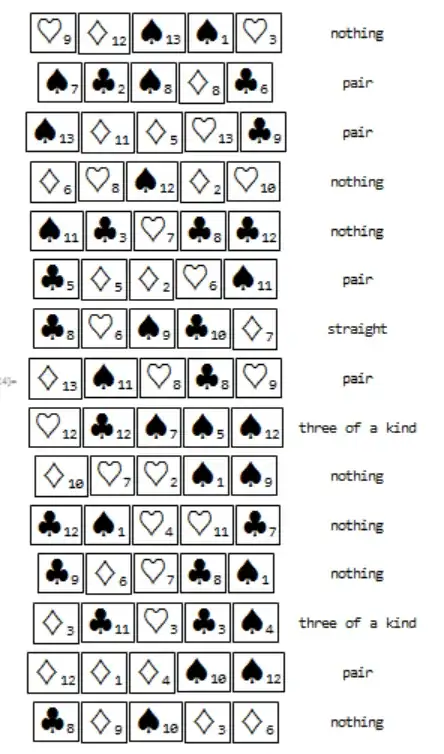
The following funcition evaluates poker hands:
f1[a_List] := Reverse /@ Map[Length, #, {2}] &@a;
f2[a_List] := Reverse /@ (Sort /@ SortBy[# /. {"A" -> 14, "J" -> 11, "K" -> 13, "Q" -> 12}, Length] & /@ (Split /@ Sort /@ Transpose[#])) &@a;
f3[a_List] := Flatten@f2[a][[2]] - 1;
f4[a_List] := f1[f2@a];
carddeck = Reverse[Flatten[Map[({{"♡", #}, {"♣", #}, {"♢", #}, {"♠", #}}) &, Join[Table[i, {i, 2, 10}], {"J", "Q", "K", "A"}]], 1]];
cardpicture[{suit_, val_}] := Framed[Column[{val, suit}, Center, 0, ItemSize -> {3/2, 1}, ItemStyle -> Directive[10, "Label", Switch[suit, "♡" | "♢", Darker[Red, 0.2], "♣" | "♠", Black]]]];
cd = Flatten[{Range@13,
SortBy[carddeck /. {"J" -> 11, "Q" -> 12, "K" -> 13, "A" -> 14}, First] /. {11 -> "J" , 12 -> "Q", 13 -> "K", 14 -> "A"}}, 1];
sc[a_List] := (a[[All, 2]] /. {"A" -> 14, "J" -> 11, "K" -> 13, "Q" -> 12}) - 1;
sortbysc[a_List] := (Transpose@(SortBy[#, First] &@Thread@{sc@a, a}))[[2]];
eph[a_List] := Module[{straight, e, f, g, pp, pl, pr, pq, q, r, s, t, u, v, w, x, y, z, q1, r1, s1, t1, u1, v1, w1, x1, y1, z1, ff, hh, jj, ll, zz},
pl = 371293; pr = 13; pq = pr; g = sortbysc@a;
straight = MemberQ[Sort /@ Take[Partition[Join[Table[i, {i, 2, 10}], {"J", "Q", "K", "A"}], 5, 1, 1], 9], Sort[Last[Transpose[a]]]];
e = f3@a; f = f4@a;
z = (pr^(-#) & /@ Range[5])(*high card*); z1 = Total[z*e];
y = (pr^(-#) & /@ {1, 1, 2, 3, 4})(*pair*); y1 = Total[y*e];
x = (pr^(-#) & /@ {1, 1, 2, 2, 3})(*two pairs*); x1 = Total[x*e];
w = (pr^(-#) & /@ {1, 1, 1, 2, 3})(*three of a kind*);
w1 = Total[w*e];
v = (pr^(-#) & /@ Range[5])(*straight*); v1 = Total[v*e];
u = (pr^(-#) & /@ Range[5])(*flush*); u1 = Total[u*e];
t = (pr^(-#) & /@ {1, 1, 1, 2, 2})(*full house*); t1 = Total[t*e];
s = (pr^(-#) & /@ {1, 1, 1, 1, 2})(*four of a kind*);
s1 = Total[s*e];
r = (pr^(-#) & /@ Range[5])(*straight flush*); r1 = Total[r*e];
q = (pr^(-#) & /@ Range[5])(*royal flush*); q1 = Total[q*e];
zz = If[g[[All, 2]] == {2, 3, 4, 5, "A"} && f[[1]] != {5}, {{19*10^6}, "straight", Flatten[{{Last@g}, Most@g}, 1]}, If[g[[All, 2]] == {2, 3, 4, 5, "A"} && f[[1]] == {5}, {{2*19*10^6}, "straight flush", Flatten[{{Last@g}, Most@g}, 1]},
If[straight,If[ f[[1]] == {5},
If[Sort[Last[Transpose[a]]] == {10, "A", "J", "K", "Q"}, {pl {8*pq + q1}, "royal flush", g}, {pl {8*pq + r1},
"straight flush", g}], {pl {4*pq + v1}, "straight", g}],
If[ f[[1]] == {5}, {pl {5*pq + u1}, "flush", g},
Switch[f[[2]],
{1, 4}, {pl {7*pq + s1}, "four of a kind", g},
{2, 3}, {pl {6*pq + t1}, "full house", g},
{1, 1, 3}, {pl {3*pq + w1}, "three of a kind", g},
{1, 2, 2}, {pl {2*pq + x1}, "two pairs", g},
{1, 1, 1, 2}, {pl {1*pq + y1}, "pair", g},
{1, 1, 1, 1, 1}, {pl {z1}, "high card", g}
]]]]]];
Something like the following then can be used to simulate a hold'em game with n players:
ff[p_Integer, li_List] :=
If[Length@li < 5, 0, N[Total[Module[{m, aa, b, cc, dd, e, f, g, h, i, t, q},
m = Take[li, 2];
f = Drop[li, 2];
aa = Partition[RandomSample[Complement[carddeck, Flatten[{m, f}, 1]]], UpTo@2];
b = Flatten[#, 1] & /@ Thread@{ConstantArray[f, p - 1], Take[aa, p - 1]};
cc = Complement[carddeck, Flatten[{Flatten[{b}, 2], Flatten[{m, f}, 1]}, 1]];
dd = RandomSample[cc, 2];
e = Flatten[{f, dd}, 1];
g = Last@Sort[Last@Sort[eph /@ Subsets[#, {5}]] & /@ (Flatten[#, 1] & /@Thread@{ConstantArray[dd, p - 1], b})];
h = Last@Sort[eph /@ Subsets[#, {5}]] &@Flatten[{m, f, dd}, 1];
i = If[g[[1, 1]] > h[[1, 1]], 0, If[g[[1, 1]] < h[[1, 1]], 1, 1/2]]] & /@ Range@100]]];
Clear[list]
list = {};
compex[n_Integer] := Quiet@Module[{},
Column@{Dynamic[If[Length@Setting@# < 5, #, Grid[{{Quiet@
ff[Last@Select[Setting@#, NumericQ], Select[Setting@#, NumericQ@# == False &]]}}, Alignment -> Left]] &@Dynamic[list], SynchronousUpdating -> False],
Grid[Partition[Table[DynamicModule[{pressed = False}, With[{idx = cd[[i]]},
Button[If[i < 14, cd[[i]], cardpicture@cd[[i]]], pressed = ! pressed;
list = If[pressed, Append[list, idx], DeleteCases[list, idx]],
Appearance -> Dynamic@If[pressed, "Pressed", Automatic]]]], {i, 65}], 13], Alignment -> Left]}];
eg
compex[5]
This is a simulation with only 100 games. Can this be sped up to give a more accurate percentage?
NB
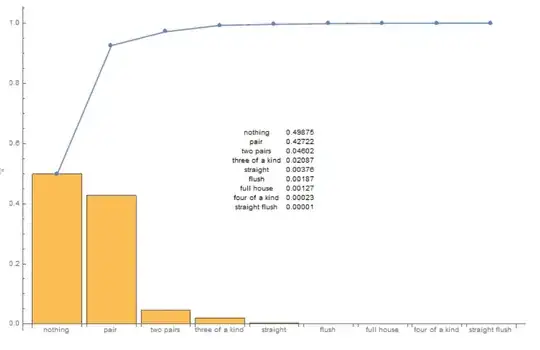
Rest /@ First /@ SplitBy[SortBy[eph /@ Subsets[carddeck, {5}], First], First]
sorts all possible 7462 possible distinct hands, but I don't know (once saved as .txt file & then imported):
ab = %;
Export["ab.txt", ab];
ab = ToExpression[Import["ab.txt", "List", CharacterEncoding -> "UTF8"]];
(since it takes a while to evaluate) whether this can be utilised to speed up the simulation.
(where up to 7 cards are selected; the first 2 being the players own hand, and the rest is the flop, river, etc., and the number pressed in the top row is the number of players in the game), which gives an approximate percentage win.
Poweris listable so you can dopr^-{1,2,3}instead ofpr^(-#)&/@{1,2,3}.z.eis usually faster thanTotal[z*e]. Treat all card values internally as numbers, only convert 11 to "J" and 12 to "Q" for display. – Simon Woods Feb 07 '17 at 21:31