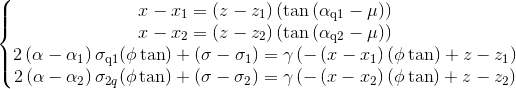Solve says my system of equations has no solution

Question

I got a system like this (just for example):

I need to get some of the variables expressed in a form like the following.

x == (z - z1) Tan[α1q - μ ] + x1

Let's say that x and σ are required. I write the following code:

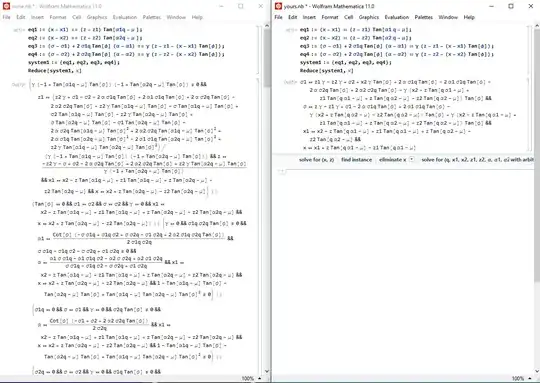
eq1 := (x - x1) == (z - z1) Tan[α1q - μ ]; 
eq2 := (x - x2) == (z - z2) Tan[α2q - μ ]; 
eq3 := (σ - σ1) + 2 σ1q Tan[ϕ] (α - α1) == γ (z - z1 - (x - x1) Tan[ϕ]); 
eq4 := (σ - σ2) + 2 σ2q Tan[ϕ] (α - α2) == γ (z - z2 - (x - x2) Tan[ϕ]); 
system1 := {eq1, eq2, eq3, eq4}; 
Solve[system1, x]

Evaluation gives me just {}. How to make this request correct?

UPD got different outputs in notebooks and none of them is what I really want.

Answer 1

Try Reduce

eq1 := (x - x1) == (z - z1) Tan[α1 q - μ];
eq2 := (x - x2) == (z - z2) Tan[α2 q - μ];
eq3 := (σ - σ1) + 
    2 σ1q Tan[ϕ] (α - α1) == γ (z - 
      z1 - (x - x1) Tan[ϕ]);
eq4 := (σ - σ2) + 
    2 σ2q Tan[ϕ] (α - α2) == γ (z - 
      z2 - (x - x2) Tan[ϕ]);
system1 := {eq1, eq2, eq3, eq4};
Reduce[system1, x]

Learning from Pros is always helpful...

Reduce[system1, x] // Union // First

x == x1 + z Tan[q α1 - μ] - z1 Tan[q α1 - μ]

Collect[%, Tan[q α1 - μ]]

x == x1 + (z - z1) Tan[q α1 - μ]

Answer 2

I think MMM is being ingenuous. Reduce returns a rather complicated expression with a lot of conditionals (24 of them). It turns out that the equation for x is same under all the conditions. So I think I need to show a little more work than MMM did.

eq1 = (x - x1) == (z - z1) Tan[α1q - μ];
eq2 = (x - x2) == (z - z2) Tan[α2q - μ];
eq3 = (σ - σ1) + 2 σ1q Tan[ϕ] (α - α1) == γ (z - z1 - (x - x1) Tan[ϕ]);
eq4 = (σ - σ2) + 2 σ2q Tan[ϕ] (α - α2) == γ (z - z2 - (x - x2) Tan[ϕ]);
system1 = {eq1, eq2, eq3, eq4};

Note I do not use := here. It is inappropriate.

xeqs = Cases[Reduce[system1, x], x == _, ∞] // Union

{x == x2 + z Tan[α2q - μ] - z2 Tan[α2q - μ]}

This last shows that there is really only one solution, so what is wanted is

xeqs[[1]]

x == x2 + z Tan[α2q - μ] - z2 Tan[α2q - μ]