Plot polygonal surface

Question

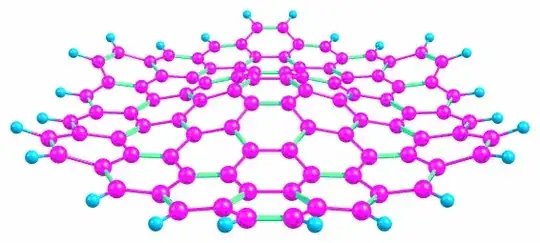
I have a list of 120 elements of the form $\{q,x,y,z\}$. In fact, each element of the represents the nuclear charge and 3 coordinates of an atom of some large molecule.

qxyz={{6, 6.10835, -0.710283, 0.211502}, {6, 7.34167, -1.43322, 0.}, {6, 7.32715, -2.79984, 0.126901}, {6, 6.11632, -3.53126, 0.296102}, {6,4.89643, -2.82695, 0.338403}, {6, 4.89915, -1.40962, 0.296102}, {6, 6.08831, -4.94558, 0.126901}, {6, 4.86614, -7.09492, -0.465304}, {6,4.91204, -5.64146, 0.}, {6, 3.6693, -4.93485, 0.211502},
{6,3.67034,-3.53798, 0.296102},{6, 8.57745, -0.666746, -0.465304}, {6, 6.08831, 4.94558, 0.126901}, {6,4.91204, 5.64146, 0.}, {6, 4.86614, 7.09492, -0.465304}, {6, 6.11632, 3.53126, 0.296102}, {6, 7.32715, 2.79984, 0.126901}, {6, 7.34167, 1.43322, 0.}, {6, 6.10835, 0.710283, 0.211502}, 
{6, 4.89915, 1.40962, 0.296102}, {6, 4.89643, 2.82695, 0.338403}, {6,3.67034, 3.53798, 0.296102}, {6, 3.6693, 4.93485, 0.211502}, {6,8.57745, 0.666746, -0.465304}, {6, -1.23884, 7.74542, 0.126901}, {6,0., 7.06252, 0.296102}, {6, 1.23884, 7.74542, 0.126901}, {6, 0., 5.65391, 0.338403}, {6, -1.22881, 4.94759, 0.296102}, {6, -2.43905, 5.64513, 0.211502}, 
{6, -2.42963, 7.07468, 0.}, {6, -3.71131, 7.76166, -0.465304}, {6, 3.71131, 7.76166, -0.465304}, {6, 2.42963, 7.07468, 0.}, {6, 1.22881, 4.94759, 0.296102}, {6, 2.43905, 5.64513,0.211502}, {6, -6.08831, 4.94558, 0.126901}, {6, -7.32715, 2.79984,0.126901}, {6, -6.11632, 3.53126, 0.296102}, {6, -7.34167, 1.43322,0.}, {6, -8.57745, 0.666746, -0.465304}, {6, -4.86614, 7.09492, -0.465304}, {6, -4.91204, 5.64146, 0.}, 
{6, -3.6693, 4.93485, 0.211502}, {6, -3.67034, 3.53798, 0.296102}, {6, -4.89643, 2.82695, 0.338403}, {6, -6.10835, 0.710283, 0.211502}, {6, -4.89915,1.40962, 0.296102}, {6, -8.57745, -0.666746, -0.465304}, {6, -7.34167, -1.43322, 0.}, {6, -7.32715, -2.79984, 0.126901}, {6, -6.11632, -3.53126,0.296102}, {6, -6.08831, -4.94558,0.126901}, {6, -6.10835, -0.710283, 0.211502}, {6, -4.89915, -1.40962, 0.296102}, {6, -4.89643, -2.82695, 0.338403}, {6, -3.67034, -3.53798, 0.296102}, 
{6, -3.6693, -4.93485,0.211502}, {6, -4.91204, -5.64146, 0.}, {6, -4.86614, -7.09492, -0.465304}, {6, -1.22881, -4.94759,0.296102}, {6, 0., -5.65391, 0.338403}, {6, 0., -7.06252, 0.296102}, {6, -1.23884, -7.74542, 0.126901}, {6, -2.42963, -7.07468, 0.}, {6, -2.43905, -5.64513, 0.211502}, {6, 1.23884, -7.74542, 0.126901}, {6, -3.71131, -7.76166, -0.465304}, {6, 1.22881, -4.94759, 0.296102}, {6,2.43905, -5.64513, 0.211502}, 
{6, 2.42963, -7.07468, 0.}, {6,3.71131,-7.76166, -0.465304}, {6, -1.22943, 3.52325, 0.0423004}, {6, 0., 2.81538, -0.253802}, {6, 0.,1.418, -0.676806}, {6, -1.22802, 0.708999, -0.676806}, {6, -2.43819,1.40769, -0.253802}, {6, -2.43651, 2.82635, 0.0423004}, {6,1.22802, 0.708999, -0.676806}, {6, -1.22802, -0.708999, -0.676806},{6, 0., -1.418, -0.676806}, {6, 1.22802, -0.708999, -0.676806}, {6,0., -2.81538, -0.253802}, 
{6, -1.22943, -3.52325,0.0423004}, {6, -2.43651, -2.82635,0.0423004}, {6, -2.43819, -1.40769, -0.253802}, {6, -3.66594,-0.696905, 0.0423004}, {6, -3.66594, 0.696905, 0.0423004}, {6,1.22943, 3.52325, 0.0423004}, {6, 2.43651, 2.82635, 0.0423004}, {6,2.43819, 1.40769, -0.253802}, {6, 3.66594, 0.696905, 0.0423004}, {6,3.66594, -0.696905, 0.0423004}, {6, 2.43819, -1.40769, -0.253802}, {6, 1.22943, -3.52325,0.0423004}, {6, 2.43651, -2.82635, 0.0423004}, {1, 5.79985,7.62243, -0.888307}, {1, 7.01997, 5.47808, -0.0423004}, {1, 8.25414,3.34043, -0.0423004}, 
{1, 9.50115, 1.21161, -0.888307}, {1, 9.50115, -1.21161, -0.888307}, {1,8.25414, -3.34043, -0.0423004}, {1, 7.01997, -5.47808, -0.0423004}, {1, 5.79985, -7.62243, -0.888307}, {1,3.70129, -8.83404, -0.888307}, {1,1.23417, -8.81851, -0.0423004}, {1,-1.23417, -8.81851,-0.0423004}, {1, -3.70129, -8.83404, -0.888307}, {1,-5.79985,-7.62243, -0.888307}, {1, -7.01997, -5.47808, -0.0423004}, {1,-8.25414, -3.34043, -0.0423004}, {1, -9.50115, -1.21161, -0.888307},{1,-9.50115, 1.21161, -0.888307}, 
{1, -8.25414, 3.34043, -0.0423004}, {1,-7.01997,5.47808, -0.0423004}, {1, -5.79985, 7.62243, -0.888307}, {1,-3.70129, 8.83404, -0.888307}, {1, -1.23417, 8.81851, -0.0423004}, {1,1.23417, 8.81851, -0.0423004}, 
{1, 3.70129, 8.83404, -0.888307}};

Let us select only the coordinates and plot the surface containing them using the 1st order interpolation:

xyz = qxyz[[All, 2 ;; 4]];
fig=ListPlot3D[xyz, 
     Mesh -> None, BoxRatios -> Automatic, Boxed -> False, 
     Axes -> False, InterpolationOrder -> 1, ColorFunction -> "Rainbow"]

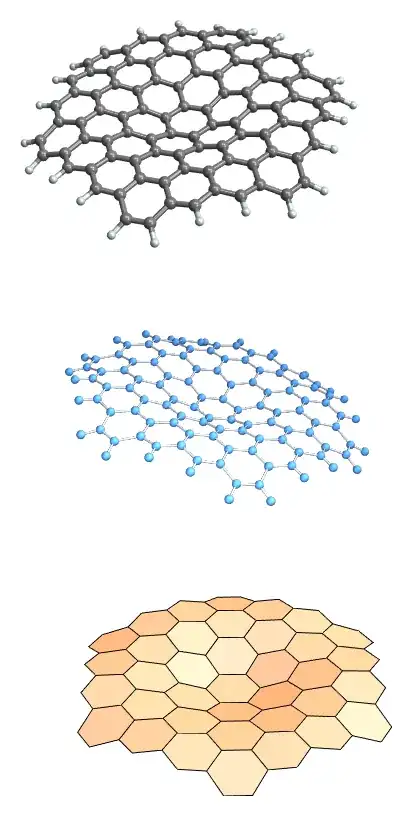
The result looks like that

Just to give you an idea how the molecule looks like

Now comes the question. I like the surface plot because it nicely depicts the vibrational mode. However, I want the surface to be composed to hexagons, like in the second picture. The hexagons' color should be a function of the hexagon's face normal, like we see in the ListPlot3D. How can I achieve this effect ? Thank you in advance.

Some of your hexagons don't lie in a single plane, and therefore the face doesn't have a well defined normal - the hexagon will have a crease down the middle. — Quantum_Oli, Feb 10 '17 at 23:09
@Quantum_Oli Indeed, good observation. Hopefully the creases will be not too pronounced — yarchik, Feb 10 '17 at 23:18

score 13 · Accepted Answer · edited Apr 13 '17 at 12:55

(grabbing a lot of code from this answer)

This is just to get you started, adding in colors to the final GraphicsComplex should be pretty easy.

xyzString = ExportString[
   qxyz /. {a_Integer, b___} :> {ElementData[a, "Abbreviation"], b},
   "Table"];
{plot, coords, atoms} = 
  ImportString[
   xyzString, {"XYZ", {"Graphics3D", "VertexCoordinates", 
     "VertexTypes"}}];
bonds = UndirectedEdge @@@ 
   Graphics`MoleculePlotDump`InferBonds[atoms, coords, 40, 25];
vertexlist = Range@Length@atoms;
chemicalGraph = 
  Graph3D[vertexlist, UndirectedEdge @@@ bonds, 
   VertexCoordinates -> coords/200];
cycles = DeleteDuplicates[Flatten[List @@@ #]] & /@ 
   FindCycle[Graph[vertexlist, UndirectedEdge @@@ bonds], {6}, All];
polygons = Graphics3D[
   GraphicsComplex[coords, Polygon[cycles]],
   Boxed -> False];
{plot, chemicalGraph, polygons}

Here's a way to add vertex colors to the polygons

cf = ColorData[{"Rainbow", MinMax[Last /@ coords]}][Last@coords[[#]]] &;
Graphics3D[
 GraphicsComplex[
  coords, {EdgeForm[Dashed], 
   Polygon[#, VertexColors -> Map[cf, #]] & /@ cycles}],
 Boxed -> False]

or as Bob shows you can combine this with a Graphics3D, like the MoleculePlot you get from the XYZ importer,

Nice and quick answer. @Quantum_Oli commented above that some polygons are not flat. Would it mean that the determination of polygons colors/shading is not so trivial? In your solution you let MA set the shading. The result is already good, and I do not think I will be able to invent a better shading. But I am wondering if the colors can be made more saturated? — yarchik, Feb 10 '17 at 23:38
@yarchik - in the edit I used the z-coordinate to color it using the VertexColors option. If you want each polygon to have just one color, that shouldn't be too hard to do — Jason B., Feb 10 '17 at 23:41
Thanks a lot. The post you liked too is also very interesting and relevant. For the shading, I found another post http://mathematica.stackexchange.com/questions/130226/polygon-mesh-compute-vertex-normals-for-smooth-shading?rq=1 where undocumented internal function Region`Mesh`MeshCellNormals[meshregion, dimension] is used. — yarchik, Feb 10 '17 at 23:50

score 9 · Answer 2 · answered Feb 10 '17 at 23:10

9

xyz = Rest /@ qxyz;

Show[
 ListPlot3D[xyz,
  Mesh -> None,
  BoxRatios -> Automatic,
  Boxed -> False,
  Axes -> False,
  InterpolationOrder -> 1,
  ColorFunction -> "Rainbow"],
 NearestNeighborGraph[xyz, {All, 1.6}]]

answered Feb 10 '17 at 23:10

Bob Hanlon

157,611
7
77
198

Although it is not exactly the visual form I had in mind, I like your idea of superimposing two objects – yarchik Feb 10 '17 at 23:24

Plot polygonal surface

2 Answers2