How can I visualize the geometry of the complex mapping $g(z)=\frac{1}{z}$?

Question

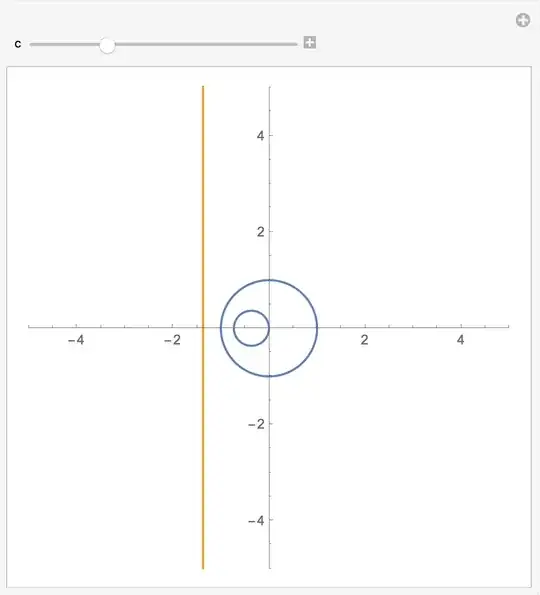
I'm trying to visualize the geometry of the complex mapping $g(z)=\frac{1}{z}$ using the following codes.

g[x_, y_] := {x/(x^2 + y^2), -y/(x^2 + y^2)};

Manipulate[ParametricPlot[{{Cos[t], Sin[t]},
   {c, 10 t},
   g[c, t]},
   {t, -Pi, Pi}, PlotRange -> {{-5, 5}, {-5, 5}}],
   {c, -3, 3}]

What I want to demonstrate is that the image of a straight line under the mapping $g$ is a circle. (And I use Manipulate to demonstrate the image for different vertical lines.) But I only get part of the circle since the straight line is actually only a segment in the plot.

Could anyone help to fix this?

I didn't mean for you to delete your question, but I couldn't spend the time to write a full answer. Hope you figured it out based on my comment. — Szabolcs, Feb 13 '17 at 20:43

A.G. · Accepted Answer · 2017-02-12T19:21:06.407

0

Not perfect but better:

g[x_, y_] := {x/(x^2 + y^2), -y/(x^2 + y^2)};

Manipulate[
 Show[
  ParametricPlot[{{Cos[t], Sin[t]}, {c, 10 t}}, {t, -Pi, Pi}, 
   PlotRange -> {{-5, 5}, {-5, 5}}],
  ParametricPlot[g[c, t], {t, -100, 100}]],
 {c, -3, 3}]

Trick: You can improve the smoothness of the parametric circle during manipulate by replacing the second plot as follows:

Manipulate[
 Show[
  ParametricPlot[{{Cos[t], Sin[t]}, {c, 10 t}}, {t, -Pi, Pi}, 
   PlotRange -> {{-5, 5}, {-5, 5}}],
  ParametricPlot[g[c, t^5], {t, -2, 2}] ],
 {{c, -1.5}, -3, 3}]

edited Feb 12 '17 at 19:21

answered Feb 12 '17 at 18:11

A.G.

4,362
13
18

1

Add PlotPoints -> 1000 in ParametricPlot for full of happiness. – user64494 Feb 12 '17 at 19:00
1

@user64494 this may be machine-dependent it does not help on my 2015 Macbook Pro. However the above added trick did. – A.G. Feb 12 '17 at 19:22
Thank you for your answer. What is the -1.5 for in {c, -1.5}, -3, 3}? – Feb 12 '17 at 22:47
Enlighten by your answer, one can replace g[c,t] with g[c,t^7] in my original code to get the desired result. – Feb 12 '17 at 22:53
1

@Jack -1.5 is the initial value of c. – A.G. Feb 12 '17 at 23:36
@A.G.: I didn't know that before. Nice to learn. Thanks! – Feb 13 '17 at 02:38

score 0 · Answer 2 · answered Feb 13 '17 at 10:52

0

f[x_, y_] := ReIm[1/(x + I y)]
Manipulate[
 ParametricPlot[{{a + b Cos[t], c + b Sin[t]}, 
   f[a + b Cos[t], c + b Sin[t]]}, {t, 0, 2 Pi}, 
  PlotRange -> {{-4, 4}, {-4, 4}}, 
  PlotLegends -> {"z", "1/z"}], {{a, 0}, -2, 2}, {{b, 1}, 0.1, 
  2}, {{c, 0}, -2, 2}]

answered Feb 13 '17 at 10:52

ubpdqn

60,617
3
59
148

I have never seen the use of ReIm before. Thanks! – Feb 13 '17 at 16:00
May I ask how you made the gif from Mathematica? – Feb 13 '17 at 16:06
@Jack I use LICECap – ubpdqn Feb 15 '17 at 07:13

How can I visualize the geometry of the complex mapping $g(z)=\frac{1}{z}$?

2 Answers2

Linked