Cutting polygons

Question

The code below was created to get a list with the coordinates of the lower left corners that will serve as a reference for my polygons

largura = 1.4; altura = 1;
col = 6; lin = 4;
p = {{0, 0}, {largura, 0}, {largura, altura}, {0, altura}};
addList = {{largura, 0}, {largura, 0}, {largura, 0}, {largura, 0}};
numSteps = col - 1;
cantosInferioresEsquerdos = Tuples[{
   Table[Plus[i], {i, 0, (col - 1) largura, largura}], 
   Table[Plus[i], {i, 0, (lin - 1) altura, altura}]}]

$\left( \begin{array}{cc} 0. & 0 \\ 0. & 1 \\ 0. & 2 \\ 0. & 3 \\ 1.4 & 0 \\ 1.4 & 1 \\ 1.4 & 2 \\ 1.4 & 3 \\ 2.8 & 0 \\ 2.8 & 1 \\ 2.8 & 2 \\ 2.8 & 3 \\ 4.2 & 0 \\ 4.2 & 1 \\ 4.2 & 2 \\ 4.2 & 3 \\ 5.6 & 0 \\ 5.6 & 1 \\ 5.6 & 2 \\ 5.6 & 3 \\ 7. & 0 \\ 7. & 1 \\ 7. & 2 \\ 7. & 3 \\ \end{array} \right)$

With the list above I created another list that defines the four corners of each polygon

positions = 
 FoldList[Plus, 
   cantosInferioresEsquerdos[[#]], {{largura, 0}, {0, altura}, {-largura, 0}}] & /@ 
      Range[Length[cantosInferioresEsquerdos]]

$\left( \begin{array}{cccc} \{0.,0\} & \{1.4,0\} & \{1.4,1\} & \{0.,1\} \\ \{0.,1\} & \{1.4,1\} & \{1.4,2\} & \{0.,2\} \\ \{0.,2\} & \{1.4,2\} & \{1.4,3\} & \{0.,3\} \\ \{0.,3\} & \{1.4,3\} & \{1.4,4\} & \{0.,4\} \\ \{1.4,0\} & \{2.8,0\} & \{2.8,1\} & \{1.4,1\} \\ \{1.4,1\} & \{2.8,1\} & \{2.8,2\} & \{1.4,2\} \\ \{1.4,2\} & \{2.8,2\} & \{2.8,3\} & \{1.4,3\} \\ \{1.4,3\} & \{2.8,3\} & \{2.8,4\} & \{1.4,4\} \\ \{2.8,0\} & \{4.2,0\} & \{4.2,1\} & \{2.8,1\} \\ \{2.8,1\} & \{4.2,1\} & \{4.2,2\} & \{2.8,2\} \\ \{2.8,2\} & \{4.2,2\} & \{4.2,3\} & \{2.8,3\} \\ \{2.8,3\} & \{4.2,3\} & \{4.2,4\} & \{2.8,4\} \\ \{4.2,0\} & \{5.6,0\} & \{5.6,1\} & \{4.2,1\} \\ \{4.2,1\} & \{5.6,1\} & \{5.6,2\} & \{4.2,2\} \\ \{4.2,2\} & \{5.6,2\} & \{5.6,3\} & \{4.2,3\} \\ \{4.2,3\} & \{5.6,3\} & \{5.6,4\} & \{4.2,4\} \\ \{5.6,0\} & \{7.,0\} & \{7.,1\} & \{5.6,1\} \\ \{5.6,1\} & \{7.,1\} & \{7.,2\} & \{5.6,2\} \\ \{5.6,2\} & \{7.,2\} & \{7.,3\} & \{5.6,3\} \\ \{5.6,3\} & \{7.,3\} & \{7.,4\} & \{5.6,4\} \\ \{7.,0\} & \{8.4,0\} & \{8.4,1\} & \{7.,1\} \\ \{7.,1\} & \{8.4,1\} & \{8.4,2\} & \{7.,2\} \\ \{7.,2\} & \{8.4,2\} & \{8.4,3\} & \{7.,3\} \\ \{7.,3\} & \{8.4,3\} & \{8.4,4\} & \{7.,4\} \\ \end{array} \right)$

The function below defines in which column I start the cut and which column I end the cut

cut[col1_, col2_] := {{(col1 - 1)*largura, 0}, {(col2 - 1)*largura, lin}}

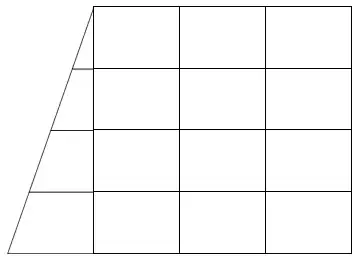
The graph below shows my polygons with the intention of cutting

Graphics[{
  t = Thickness[0.002],
  EdgeForm[t],
  White,
  Polygon[positions],
  Red,
  Dashed,
  Line[cut[3, 4]]
  },
 ImageSize -> 1160]

The question is this:

Is there a command where I can cut my polygons in order to get "fractional" polygons?

Your function cut calculates the positions of the "cutting points". Couldn't you simply generate a Polygon object knowing from Polygon@Flatten@{top-left, bottom-left, cut[col1, col2]}? — MarcoB, Feb 16 '17 at 17:42
You could rewrite this question to be very precise and interesting: Given a Polygon and a line that bisects that polygon, either a Line or InfiniteLine, how to split the Polygon into 2. The rest of the code is specific to your situation and makes the question less general. (and then I google this question to find it's been asked here) — Jason B., Feb 16 '17 at 18:18
Are you only concerned with cutting a rectangular grid or do you need to be more general? — george2079, Feb 16 '17 at 23:35
In a few hours I will be prepared to evaluate the comments. Thank you very much so far. — LCarvalho, Feb 17 '17 at 00:44

score 4 · Accepted Answer · answered Feb 16 '17 at 21:15

Just to show how you might implement this here,

polygons = Polygon /@ positions;
plane = HalfPlane[cut[3, 4], {10, 0}];
polygons2 = 
 RegionIntersection[#, plane] & /@ polygons // 
  DeleteCases[_EmptyRegion | _Point]

(* {Polygon[{{2.8, 0.}, {4.2, 0.}, {4.2, 1.}, {3.15, 1.}}], 
 Polygon[{{3.15, 1.}, {4.2, 1.}, {4.2, 2.}, {3.5, 2.}}], 
 Polygon[{{3.5, 2.}, {4.2, 2.}, {4.2, 3.}, {3.85, 3.}}], 
 Triangle[{{3.85, 3.}, {4.2, 4.}, {4.2, 3.}}], 
 Rectangle[{4.2, 0.}, {5.6, 1.}], Rectangle[{4.2, 1.}, {5.6, 2.}], 
 Rectangle[{4.2, 2.}, {5.6, 3.}], Rectangle[{4.2, 3.}, {5.6, 4.}], 
 Rectangle[{5.6, 0.}, {7., 1.}], Rectangle[{5.6, 1.}, {7., 2.}], 
 Rectangle[{5.6, 2.}, {7., 3.}], Rectangle[{5.6, 3.}, {7., 4.}], 
 Rectangle[{7., 0.}, {8.4, 1.}], Rectangle[{7., 1.}, {8.4, 2.}], 
 Rectangle[{7., 2.}, {8.4, 3.}], Rectangle[{7., 3.}, {8.4, 4.}]} *)

Note that RegionIntersection is programmed to be smart enough to recognize when a region is a Triangle or Rectangle. But if we look at the result,

Graphics[{EdgeForm@Thickness[0.002], White, polygons2}]

Mathematica graphics

you can see that the Rectangle handles the perimeter drawing differently than the Polygon and Triangle primitives. So just convert them all to Polygon:

polygons2 = 
  ReplaceAll[{Triangle[a_] :> Polygon[a], 
     Rectangle[{xmin_, ymin_}, {xmax_, ymax_}] :> 
      Polygon[{{xmin, ymin}, {xmax, ymin}, {xmax, ymax}, {xmin, 
         ymax}}]}]@polygons2;

Graphics[{EdgeForm@Thickness[0.002], White, polygons2}]

Mathematica graphics

Cutting polygons

1 Answers1