3

I'm trying to get an intersection boundary of a prism's surface and a plane:

prism = Entity["Polyhedron",{"Prism", 6}]
plane = InfinitePlane[prism["VertexCoordinates"][[{4, 6, 11}]]]

RegionIntersection[plane, prism["ImplicitRegion"]]

DiscretizeRegion turns it into 2D face, but I can't for the life of me extract the boundary of it. RegionBoundary doesn't work, it works as an identity and doesn't lower region's dimension. I've also tried everything with prism["MeshRegion"] and prism["BoundaryMeshRegion"].

swish
  • 7,881
  • 26
  • 48
  • 1
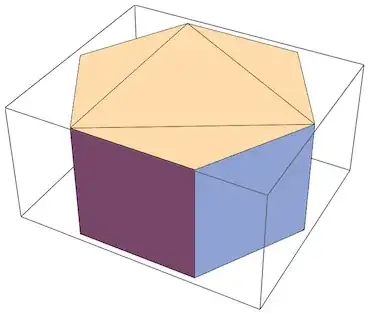
    Wow, I was going to suggest you use the method described here to get the intersection - and it would in principle work. But if you execute Length[MeshPrimitives[ EntityValue[ Entity["Polyhedron", {"Prism", 6}], "MeshRegion"], 2] ] you see that the mesh region for this entity has almost 24,000 polygons! – Jason B. Feb 17 '17 at 23:13
  • @JasonB. It kinda works Cases[RegionIntersection[plane, #] & /@ MeshPrimitives[DiscretizeGraphics@prism["Faces"], 2], _Line], not exactly perfect, but good enough... – swish Feb 17 '17 at 23:25
  • 1
    Still would love some Region solution, discretizing graphics feels wrong to me – swish Feb 17 '17 at 23:29
  • in general Region functions don't work for 3D regions as well. You can tweak your solution to give a polygon, polygon = Cases[RegionIntersection[plane, #] & /@ MeshPrimitives[DiscretizeGraphics@prism["Faces"], 2], Line[{a_, b_}] :> Sequence[a, b]] // (#[[Last@FindShortestTour[#]]] &) // Polygon; Graphics3D@polygon – Jason B. Feb 17 '17 at 23:43
  • 1
    @JasonB. Luckily for us, the "BoundaryMeshRegion" property gives us a region with a minimal amount of polygons. We can get a MeshRegion from this with only 12 tetrahedron with TriangulateMesh[prism["BoundaryMeshRegion"], MaxCellMeasure -> Infinity]. – Greg Hurst Feb 20 '17 at 14:18

1 Answers1

3

A potential work around is to express this region in terms of graphics regions.

prism = Entity["Polyhedron", {"Prism", 6}];
plane = InfinitePlane[prism["VertexCoordinates"][[{4, 6, 11}]]];

pts = prism["VertexCoordinates"];

prisms = Prism[pts[[#]]] & /@ {{1, 3, 5, 2, 4, 6}, {5, 9, 11, 6, 10, 12}, 
  {7, 3, 11, 8, 4, 12}, {3, 5, 11, 4, 6, 12}};

Graphics3D[prisms]

enter image description here

ints = RegionIntersection[#, plane] & /@ prisms

{
  Line[{{-1/2, -Sqrt[3]/2, 1/2}, {-1/2, Sqrt[3]/2, 1/2}}], 
  Triangle[{{-1/2, Sqrt[3]/2, 1/2}, {1/2, Sqrt[3]/2, -1/6}, {1, 0, -1/2}}], 
  Triangle[{{-1/2, -Sqrt[3]/2, 1/2}, {1, 0, -1/2}, {1/2, -Sqrt[3]/2, -1/6}}], 
  Triangle[{{-1/2, -Sqrt[3]/2, 1/2}, {-1/2, Sqrt[3]/2, 1/2}, {1, 0, -1/2}}]
}

final = Polygon[Rest[ints][[All, 1]]];

Graphics3D[final]

enter image description here

At this point one could figure out a way to merge the three triangles into a 5 sided polygon.

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136