12

Say I want to define a custom graphical representation for my function foo. I can do this using MakeBoxes as in the following:

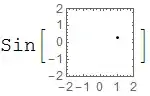
foo /: MakeBoxes[foo[x_, y_], StandardForm] := ToBoxes @ Graphics[{
    Point@{x, y}
  }, Frame -> True, PlotRange -> {{-2, 2}, {-2, 2}}
]

so that evaluating foo[1, 1.5] produces a Graphics object accordingly. This also works consistently if another function foobar is defined to act on a foo object, like in

foobar[foo[x_, y_]] := (Print["Matched"]; x + y)

There is another way to achieve the same result, which is using Interpretation. I could define foo2 as

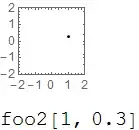
foo2[x_, y_] := Interpretation[
    Graphics[{
        Point@{x, y}
      }, Frame -> True, PlotRange -> {{-2, 2}, {-2, 2}}
    ],
    foo2[x, y]
]

This produces the same result, and works consistently when defining another function like

foobar2[foo2[x_, y_]] := (Print["Matched"]; x + y)

I (vaguely) know that Interpretation produces an InterpretationBox, so I'm guessing there should be fundamental differences between this and the result of using MakeBoxes, but I don't know what they are exactly. What are the circumstances in which one function should be preferred with respect to the other? And what the intrinsic differences?

glS
  • 7,623
  • 1
  • 21
  • 61

2 Answers2

10

Assuming that you want to create a special display form for foo that can be used in all contexts, you should use neither of these solutions. Why?

  • MakeBoxes controls how foo will be formatted. This is part of what you want. But the way you used it, the formatting is one-way. It will not be possible to convert the already formatted output as a foo expression. For example, if you edit the output cell directly, or by copying the output and paste it elsewhere, it will behave as Graphics and not as foo.

  • Interpretation is meant for typesetting only, and cannot be used in normal calculations. Interpreation["two", 2] will format in a special way so that if you copy the formatted output, and paste it elsewhere, it will look like "two", but it will behave like 2. However, if you do not format it inside of a notebook and then copy it, it will not be possible to use it as a substitute for 2. For example, Head@Interpretation["two", 2] will return Interpretation and not Integer. Thus, before Interpretation will start behaving equivalently to its second argument in computations, you must display it, then copy the displayed form.

What should you use then?

I suggest you use a specific combination of MakeBoxes and Interpretation that I presented here. This will work both ways:

  • It formats the expression in a graphical way
  • The formatted expression can be turned back into a computable expression (with head foo)

Example:

MakeBoxes[expr : foo3[x_, y_], StandardForm | TraditionalForm] := 
 ToBoxes@Interpretation[
   Graphics[{Point@{x, y}}, Frame -> True, PlotRange -> {{-2, 2}, {-2, 2}}], 
   expr
 ]

Under the hood, this creates an InterpretationBox. InterpretationBox is a special box form that already contains the expression it represents. Thus you do not need to create an explicit back-conversion rule using MakeExpression.

The above could also be written as

MakeBoxes[expr : foo3[x_, y_], StandardForm | TraditionalForm] := 
  With[{boxes = ToBoxes@Graphics[{Point@{x, y}}, Frame -> True, PlotRange -> {{-2, 2}, {-2, 2}}]}, 
    InterpretationBox[boxes, expr]
  ]

This form will sometimes give more flexibility.

With foo3 you can do the following:

enter image description here

Neither of the two approaches you describe (foo and foo2) will behave this way.

Community
  • 1
Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • Related: (4112299) – Mr.Wizard Feb 19 '17 at 16:07
  • I tend to vote for your answers a lot but in this case I hesitate to. This doesn't appear to me to be an answer to this question. Can you convince me otherwise? – Mr.Wizard Feb 19 '17 at 16:08
  • 1
    @Mr.Wizard Maybe tomorrow, I should be doing something else right now ... will log off. Perhaps OP can comment is this is useful at all and I will edit or delete the answer tomorrow. – Szabolcs Feb 19 '17 at 16:10
  • 1
    @Mr.Wizard I see your point, but perhaps the question poses a false dichotomy. The question asks whether to use MakeBoxes or Interpretation. But the two are normally used together, as illustrated by this response. I suggest that Interpretation does not have much use outside of typesetting because the wrapper just "gets in the way". (Incidentally, I tend to use higher level UI constructs like Interpretation over lower level box constructs like InterpretationBox, but that is just a matter of taste.) – WReach Feb 19 '17 at 16:30
  • @Szabolcs I'm not sure I understand your second point. If I do var = foo[1, 1.5]; Head @ var I get foo – glS Feb 19 '17 at 16:48
  • I find this answer very interesting, even if maybe it approaches the question less directly that Mr.Wizard's one. It shows a better way to use MakeBoxes and Interpretation together – glS Feb 19 '17 at 16:51
  • @glS He means if you copy the output and try to use it as input. That is what this answer is about. – Mr.Wizard Feb 20 '17 at 07:03
  • @Mr.Wizard but the way I understood it, that's the third point. The second point states that evaluating Head on the output of foo[1, 1.5] does not give foo, but this is not the case, is it? – glS Feb 21 '17 at 09:50
  • @glS (and Mr.W) Sorry for the late response. My point was that although your use case was not fully clear to me, it was my impression that you should use neither of those two approaches. As WReach said, Interpretation (foo2) is for typesetting. You would use it only if you plan to copy the result manually (copy and paste) and re-use it. Your MakeBoxes solution is fine for as long as you do programmatic manipulations only (e.g. var = foo[...]), but it won't allow you to copy and re-use the output. Or to edit the output cell and do something with the output. – Szabolcs Feb 21 '17 at 13:46
  • @glS My solution will let you use the result in either of those ways: you can assign it to a variable programmatically and use it, or use it as a sub-part of a larger expression. But you can also start typing in the output cell and re-use the result there. Or copy and paste the output into another expression and re-use it. You can do this with foo3 but you cannot do this with foo. – Szabolcs Feb 21 '17 at 13:47
  • 1
    @Mr.Wizard I rewrote the answer, hope it's clearer. – Szabolcs Feb 21 '17 at 14:28
  • @Szabolcs thanks, I see your point more clearly now (even though I didn't question the usefulness of the answer also for the previous version!). So am I understanding correctly that the only reason Interpretation does not work like your version is that it must be printed on a notebook for it to be converted into an InterpretationBox, which instead works as we want? – glS Feb 21 '17 at 15:16
  • 1
    @glS Yes, you could put it that way. To be honest, I never really understood what Interpretation was good for in practice, when used on its own (without MakeBoxes). But I am sure that there are some good uses that I have not thought of. – Szabolcs Feb 21 '17 at 15:18
  • You've got my vote now. :-) – Mr.Wizard Feb 21 '17 at 18:01
  • @Szabolcs, If foo with its parameters is a Function, eg, foo[x_, y_] := (x + y + #) &, then it seems to ignore the MakeBoxes upvalue. Can you reproduce this and if so is there a workaround? – alancalvitti Aug 17 '19 at 17:28
  • @Szabolcs, to clarify, I substituted SuscriptBox for Graphics, eg foo /: MakeBoxes[c : foo[x_, y_], form : (StandardForm | TraditionalForm)] := With[{boxes = SubscriptBox[x, y]}, InterpretationBox[boxes, c]] – alancalvitti Aug 17 '19 at 17:30
  • @alancalvitti It would immediately evaluate to a Function[...], which does not have formatting rules. To keep the formatting, use sub-values, i.e. define foo[x_, y_][args_] := .... Or am I misunderstanding your question? – Szabolcs Aug 17 '19 at 18:56
  • @Szabolcs, understood. However, foo[x_, y_][args_] seems to work when x ,y are numbers, but for example foo[a,b] where a and b are undefined symbols evaluates to expressions involving $CellContext, or gives an error with expressions like foo[{1,2},3]: An unknown box name List was sent as the BoxForm for an expression... – alancalvitti Aug 18 '19 at 13:22
9

Point of conversion

A large and perhaps key difference is that MakeBoxes (foo) only transforms the expression into the expanded form when it is converted to Box form. It's FullForm remains unchanged.

foo[1, 0.3] // InputForm

foo[1, 0.3`]

This means that you can operate upon the expression in every standard way without thought to a hidden internal format.

Sin /@ foo[1, 0.3`];
%[[2]]

0.29552

Interpretation (foo2) does not allow this:

Sin /@ foo2[1, 0.3`];
%[[2]]

enter image description here

The cause:

Sin /@ foo2[1, 0.3`] // InputForm

Interpretation[
 Sin[Graphics[{Point[{1, 0.3}]}, Frame -> True, PlotRange -> {{-2, 2}, {-2, 2}}]], 
 Sin[foo2[1, 0.3]]]

Held expressions

Another difference manifests when these expressions are wrapped in Hold constructs. Because MakeBoxes works outside the standard evaluation sequence the graphic still displays. foo2 however must evaluate before Interpretation is even part of the expression.

HoldForm[ foo[1, 0.3] ]

HoldForm[ foo2[1, 0.3] ]

enter image description here

Related to this point: Prevent graphics render inside held expression

Community
  • 1
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371