Summing elements in a list by groups indicated by a list of indices

Question

I have two lists, one containing values, the other indices. Now I want to accumulate the values that have the same corresponding index. So for example:

values  = {2, 6, 3, 8, 3, 1, 3, 7, 1, 3, 5}

indices = {1, 3, 1, 2, 3, 1, 1, 2, 3, 2, 1}

should give

result = {2 + 3 + 1 + 3 + 5, 8 + 7 + 3, 6 + 3 + 1}

I need to do this for very large lists, so it should be efficient.

Any ideas?

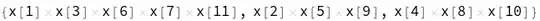
GatherBy[Transpose[{values, indices}], Last][[All, All, 1]] — user1066, Feb 20 '17 at 14:11
What's "very large lists"? Thousands of elements? Millions of elements? Billions? And how many distinct indices would be expected? 50% of elements? 10%? 1%? There will be very different ways of doing this depending on such things. — ciao, Feb 20 '17 at 14:20

score 7 · Answer 1 · answered Feb 20 '17 at 13:58

7

Pick is usually fast, and parallel processing may help, depending on your computer.

ParallelTable[Total[Pick[values, indices, k]], {k, Union[indices]}]

answered Feb 20 '17 at 13:58

KennyColnago

15,209
26
62

score 6 · Answer 2 · answered Feb 20 '17 at 15:14

6

Another possibility which is certainly quick for large sets:

GroupBy[Transpose[{values, indices}], Last -> First, Total]

This returns an association which can be converted back to a list ordered by index for no overhead with the frustratingly verbose

Normal@*SparseArray@*Normal@GroupBy[...]

answered Feb 20 '17 at 15:14

Quantum_Oli

7,964
2
21
43

1

+1 Values@GroupBy[...] will also do the trick. – WReach Feb 20 '17 at 16:57
It will, but it won't guarantee that the values will be in the order dictated by indices. SparseArray is useful as it takes care of that. – Quantum_Oli Feb 20 '17 at 17:06
Yes, you are right... the implicit ordering of various association-related operations is unreliable as it has changed over the past few releases. Values@KeySort@GroupBy[...] is another possibility. – WReach Feb 20 '17 at 17:15

score 5 · Answer 3 · edited Apr 13 '17 at 12:56

5

Possible duplicate of How to efficiently find positions of duplicates? or Gather list elements by labels

e.g.

positionDuplicates[list_] := GatherBy[Range@Length[list], list[[#]] &]

values[[#]] & /@ positionDuplicates[indices]

Total[%, {2}]

{{2, 3, 1, 3, 5}, {6, 3, 1}, {8, 7, 3}}
{14, 10, 18}

edited Apr 13 '17 at 12:56

Community

1

answered Feb 20 '17 at 14:41

Mr.Wizard

271,378
34
587
1,371

score 3 · Answer 4 · answered Feb 21 '17 at 06:15

3

A Reap/Sow variant:

Reap[MapThread[Sow[#1, #2] &, {values, indices}], _, {#2, Total@#2} &][[-1]]

yields:

{{{2, 3, 1, 3, 5}, 14}, {{6, 3, 1}, 10}, {{8, 7, 3}, 18}}

answered Feb 21 '17 at 06:15

ubpdqn

60,617
3
59
148

score 2 · Answer 5 · answered Jan 11 '24 at 00:11

values = {2, 6, 3, 8, 3, 1, 3, 7, 1, 3, 5};

indices = {1, 3, 1, 2, 3, 1, 1, 2, 3, 2, 1};

Requested result

result = {2 + 3 + 1 + 3 + 5, 8 + 7 + 3, 6 + 3 + 1}

{14, 18, 10}

Using Merge

KeySort @ Merge[Total] @ Thread[indices -> values]

<|1 -> 14, 2 -> 18, 3 -> 10|>

Values[%]

{14, 18, 10}

score 2 · Answer 6 · answered Jan 11 '24 at 00:34

groupMap = Extract[#, Map[List]@Values@PositionIndex@#2, #3] &;

Examples:

values = {2, 6, 3, 8, 3, 1, 3, 7, 1, 3, 5};
indices = {1, 3, 1, 2, 3, 1, 1, 2, 3, 2, 1};
groupMap[values, indices, Total]

{14, 10, 18}

groupMap[Array[x, Length@indices], indices, Apply[Times]]

score 1 · Answer 7 · answered Jan 11 '24 at 21:22

1

Using SplitBy:

values = {2, 6, 3, 8, 3, 1, 3, 7, 1, 3, 5};
indices = {1, 3, 1, 2, 3, 1, 1, 2, 3, 2, 1};
Total /@ Values@SplitBy[Sort@Thread[indices -> values], First]
({14, 18, 10})

answered Jan 11 '24 at 21:22

E. Chan-López

23,117
3
21
44

Summing elements in a list by groups indicated by a list of indices

7 Answers7