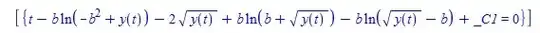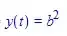2

I am trying to solve the following nonlinear, non-homogeneous, first order ODE:

$y'(t)=\sqrt{y(t)}-B$

$y(0)=B^2$

$B=const$

In code:

Y[t_] = Y[t] /. DSolve[{Y'[t] == Sqrt[Y[t]] - Bb, Y[0] == Bb^2}, Y, t]

When I evaluate the solution at t=0 I see that the initial conditions are not satisfied.

This is my code: My code

Any ideas how to solve this equation analytically (preferably, but not necessarily with Mathematica)?

Thanks in advance!

user64860
  • 121
  • 3
  • Try the method of separation of variables. You will get an implicit equation of the form f(y,t)=0. – Dimitris Feb 28 '17 at 17:24
  • As the warning suggested, Mathematica lost some solutions during the calculation. ProductLog is the principal branch of the inverse function of x Exp[x], and the other branch (denoted as f for convenience), when t=0, f[-2 Exp[-2]], equals -2. Thus Y[0]=Bb^2 (1-2)^2= Bb^2. Conclusion is that Mathematica is giving the wrong branch of the solution, but I have no idea on why it fails to give the trivial one. – W.Mason Mar 01 '17 at 15:50
  • How would I go about finding the other solutions? – user64860 Mar 02 '17 at 17:17

2 Answers2

5

One way to solve this is to ask Mathematica to solve it for general boundary conditions, and then specialize to the case you're actually interested in:

ClearAll[Y, Bb, t]
Y[t_] = Y[t] /. DSolve[{Y'[t] == Sqrt[Y[t]] - Bb, Y[0] == Cc^2}, Y, t] // Simplify;
Y[t] /. Cc -> Bb
N[% /. t -> 0]

(* {Bb^2 (1 + ProductLog[-2 E^((-4 Bb + t)/(2 Bb))])^2, Bb^2} *
(* {0.35239 Bb^2, Bb^2} *)

The first solution here is the one you already found. The second one is new, and is in fact a valid solution for the initial conditions $y(0) = B$.

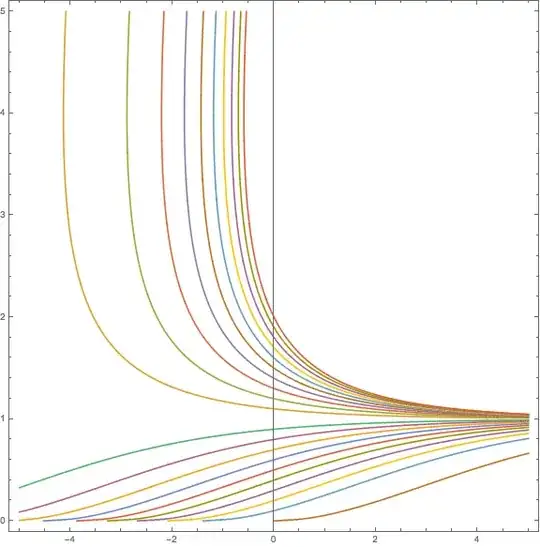
In fact, the only valid solution of your equation with the initial conditions $y(0) = B$ is $y(t) = B$. This can be seen by performing a separation of variables and integrating; we obtain the implicit solution $$ 2 (\sqrt{y} - \sqrt{y_0}) - 2 B \ln \left(\frac{\sqrt{y} - B}{\sqrt{y_0} - B} \right) = t, $$ where we use the general boundary condition $y(0) = y_0$. It can easily be seen that this equation cannot be satisfied if $y_0 = B^2$. (The separation-of-variables method assumes that $\sqrt{y} - B \neq 0$, so the trivial solution evades this problem.) Plotting the above contours for $B = 1$ also makes it pretty evident that the only solution for $y(0) = B$ is the trivial solution $y(t) = B$.

ContourPlot[Evaluate[Table[2 (Sqrt[y] - Sqrt[y0]) - 2 Log[(Sqrt[y] - 1)/(Sqrt[y0] - 1)] == x, {y0, -2, 2, 0.1}]], {x, -5, 5}, {y, 0, 5}, 
  PlotPoints -> 100, ImageSize -> Large, Axes -> True]

enter image description here

Michael Seifert
  • 15,208
  • 31
  • 68
  • 1
    I should add that I'm not sure why Mathematica fails to find the solution Y[t] = Bb when the original code is input. My guess is that there's something odd going on with the inversion algorithm going from the implicit solution to the explicit solution in terms of ProductLog; it may be a bug that should be reported to Wolfram Research. – Michael Seifert Mar 01 '17 at 13:51
2

Comment

Maple

Maple gives unexpectedly, a very simple solution (the trivial one).

restart;
ode:= diff(y(t),t)=sqrt(y(t))-b

first try without the initial condition,

dsolve(ode);

enter image description here

Which show that this ode has only implicit solution.

Now try with the initial condition,

dsolve({ode,y(0)=b^2});

enter image description here

The point, I am trying to make is, why Mathematicas DSolve is unable to produce this trivial solution?

Mathematica

I used Michael E2 proposed technique to find a series solution to the ode, which give me the trivial solution too,

seriesDSolve[y'[x] - Sqrt[y[x]] == -b, y, {x, 0, 5}, {y[0] -> (b)^2}];
Normal[%] // PowerExpand

b^2

Community
  • 1
zhk
  • 11,939
  • 1
  • 22
  • 38
  • That is indeed a solution, but it is the trivial solution i.e. y=const. But thank you anyways! – user64860 Feb 28 '17 at 17:18
  • @user64860 That's right!. Apart from the trivial solution, this ode has only implicit solution. – zhk Feb 28 '17 at 17:20
  • @corey979 it display on my web just fine. I don't know whats the issue. – zhk Feb 28 '17 at 18:58
  • Well, Mathematica's result shows that the solution can be rewritten in ProductLog (LambertW), but Mathematica uses the wrong branch in this case. – W.Mason Mar 01 '17 at 15:32