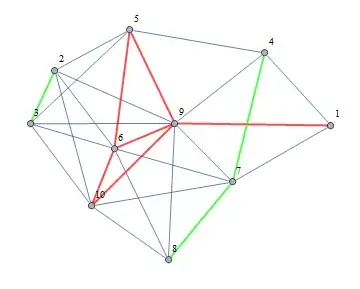
I've got a graph g with the following adjacency matrix:
adj = {{0, 0, 0, 1, 0, 0, 1, 0, 1, 0},
{0, 0, 1, 0, 1, 1, 0, 0, 1, 1},
{0, 1, 0, 0, 1, 1, 0, 0, 1, 1},
{1, 0, 0, 0, 1, 0, 1, 0, 1, 0},
{0, 1, 1, 1, 0, 1, 0, 0, 1, 0},
{0, 1, 1, 0, 1, 0, 1, 1, 1, 1},
{1, 0, 0, 1, 0, 1, 0, 1, 1, 1},
{0, 0, 0, 0, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 0, 1},
{0, 1, 1, 0, 0, 1, 1, 1, 1, 0}};
g = AdjacencyGraph[adj, VertexLabels -> "Name"]
Now I have list A, which contains mutually disjoint sets of vertices, such that no two vertices in one of the sets share an edge:
A = {{3, 4, 8}, {1, 5, 10}}
In other words, the subgraphs spanned by each of these subsets contain no edges.
And I've also got a list B which contains the remaining vertices:
B = {2, 6, 7, 9}
Now I want to add the vertices from B to the subsets in A such that the total number of edges in the subgraphs spanned by the resulting subsets is minimal. For example, if I were to add 2 to the set {3, 4, 8} the resulting subgraph would contain a single edge, but adding it to {1, 5, 10} instead would result in a subgraph with two edges.
For this example, the optimal solution is to add 2 and 7 to the first set, and 6 and 9 to the second, resulting in only 9 edges in both subgraphs together.
Is there a simple and efficient way to compute an optimal solution this problem?