0

I would like to interpolate the following function

 g[z_, e_] := 
     PDF[TruncatedDistribution[{e - 2, e + 2}, 
       NormalDistribution[e, 0.3]], z]

    a1 = N[g[-2, 0]];
    a2 = N[g[-1, 0]];
    a3 = N[g[0, 0]];
    a4 = N[g[1, 0]];
    a5 = N[g[2, 0]];

With your help I am now using:

 k[x_, e_] = 
      Interpolation[{{-2 + e, a1}, {-1 + e, a2},  {0 + e, 
     a3}, {1 + e, a4}, {2 + e, a5}}, 
   Method -> "Spline"] [x];

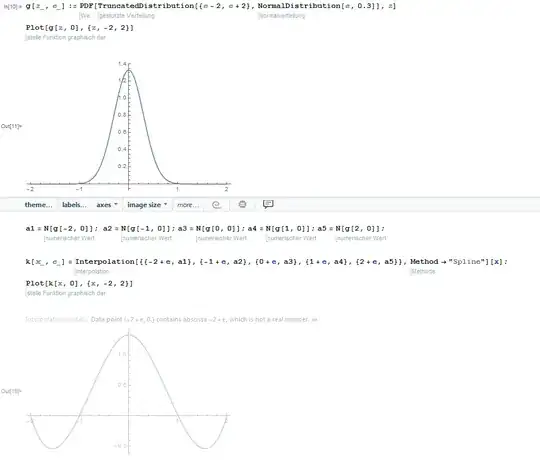enter image description here I need e as an variable, which I can easily access. Can i somehow get rid of the error shown in the picture? Or do I have to stick to InterpolatingPolynomial? Can i somehow abuse InterpolatingFunction?

Why do i get negative values in the approximation function? Can i get rif of them with other, better methods?

user34047
  • 335
  • 2
  • 7
  • 2
    Interpolation[data, Method -> "Spline"]? – vapor Mar 13 '17 at 11:47
  • have a look at 15879 – vapor Mar 13 '17 at 11:52
  • 2
    You can take derivatives with that function, and you can get a BSplineFunction with explicit parameters, what else do you want? – vapor Mar 13 '17 at 12:24
  • The suggestion of @happyfish works for me: http://i.stack.imgur.com/3horZ.png – Michael E2 Mar 13 '17 at 12:33
  • I tested the code of the thread you mentioned: points = {{-2, 2}, {2, 2}, {6, 6}, {10, 7}, {14, 11}, {18, 2}, {22, 1}, {26, 2}, {30, 1}, {34, 1}}; g = BSplineFunction[points] When i now enter g[2], or D[g[t],t] nothing happens. I am little bit lost, sry. – user34047 Mar 13 '17 at 12:34
  • Maybe you mean you want to differentiate w.r.t. e? You can numerically differentiate: http://i.stack.imgur.com/bxKjR.png – Michael E2 Mar 13 '17 at 12:34
  • Thank you for your help. I build in your proposal in my first post and clarfied my problems there. – user34047 Mar 13 '17 at 13:35
  • your k needs to be set delayed: k[x_, e_] := .... For good measure you might want to do k[x_, e_?NumericQ] := ... – george2079 Mar 13 '17 at 14:05
  • 1
    as to why you get negative values, its because you are doing a polynomial interpolation of something that's not a polynomial, with far too few points. You might have a look at FunctionInterpolation, or set InterpolationOrder->1 – george2079 Mar 13 '17 at 15:18
  • (1) The error message can be ignored in this case. (2) Why not use the formula returned by PDF[TruncatedDistribution[{e - 2, e + 2}, NormalDistribution[e, 3/10]], z] or by PDF[TruncatedDistribution[{e - 2, e + 2}, NormalDistribution[e, 0.3]], z]? – Michael E2 Mar 17 '17 at 22:49

1 Answers1

2

This is where a monotonic interpolation method like Steffen's interpolation or Fritsch-Carlson interpolation is useful. Using the routine from this answer:

k[x_, e_] := SteffenInterpolation[{{-2 + e, a1}, {-1 + e, a2}, {0 + e, a3},
                                   {1 + e, a4}, {2 + e, a5}}][x]

Plot[k[x, 0], {x, -2, 2}]

monotonic interpolant

Community
  • 1
J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574