5

Say I have a set of differential equations not necessarily in first order form. I would like to build the corresponding state space model. When equations are many and long, it becomes difficult to track how the function changes the variables names. In the documentation an example for labeling state space models is provided. Yet in the example the function does not convert an ODE. Say I have the following ODE system (just an example taken from documentation):

NonlinearStateSpaceModel[m x''[t] + c x'[t] + k[x[t]] x[t] == F[t], 
 x[t], F[t], x[t], t]

How can I automatically ask Mathematica to label the state space variable such that I can keep trace of the step "functions" used to first orderize the ODE? Note in this case it may be simple, but I'm handling in my real problem 15 ODEs among whom 12 are second order and the remaining are first order.

This is particularly troubling when one want to test a feedback law calculated with one system onto another system.

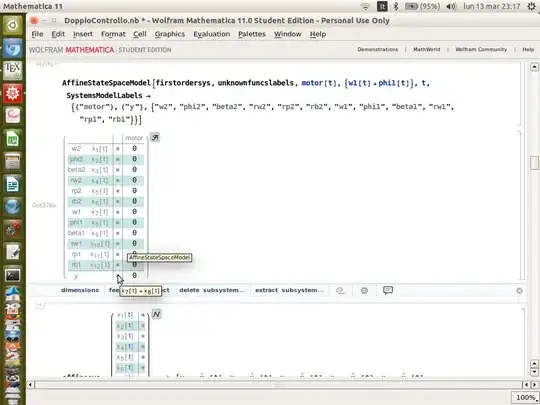
Update I see Suba's answer works good generally. Yet in my problem I still have an odd behavior I simply can't explain. I'm I getting something wrong? The output clearly should be w1+phi1... why does it show rb1???

UPDATE

I've tried the following. First use the firstorderize[] function described by Michael_E2 here 

    Options[firstOrderize] = {"NewSymbolGenerator" -> (Unique["y"] &)};
firstOrderize[sys_, vars_, t_, OptionsPattern[]] := 
 Module[{fop, newsym, toNewVar}, 
  newsym = OptionValue["NewSymbolGenerator"];
  fop = Internal`ProcessEquations`FirstOrderize[sys, {t}, 1, vars];
  If[newsym === Automatic,(*don't rename*)
   Flatten@fop[[1 ;; 2]],(*rename*)
   toNewVar = 
    With[{newvars = MapIndexed[newsym, fop[[3]], {2}]}, 
     Internal`ProcessEquations`FirstOrderReplace[#, {t}, 1, vars, 
       newvars] &];
   Flatten@{toNewVar[fop[[1]] /. Last[fop]], 
     Activate[
      toNewVar[Inactivate[Evaluate@fop[[2]], Derivative]] /. 
       toNewVar[fop[[4]]]]}]]

Secondly order the labels with SystemsModelLabels but keep in mind that the function wants in order first the labels of the "step functions" developed first orderizing, then the other labels.

Attempt

Still something doesn't work out: the column that should contain the input is a null vector. Why???? Plus, it apparently swapped the third equation with the 6th!

Community
  • 1
Mirko Aveta
  • 2,192
  • 11
  • 26

1 Answers1

3
states = {x1, x2}; 
NonlinearStateSpaceModel[
NonlinearStateSpaceModel[m x''[t] + c x'[t] + k[x[t]] x[t] == F[t], 
x[t], F[t], x[t], t], states]

enter image description here

Update

(Pseudo code to order the state names correctly)

List of all the states and the new names you want to give them.

vars = {w[t], phi[t], beta[t], rw[t], rp[t], rb[t]};
allVars = Riffle[vars, D[vars, t]];
newNames = {w1[t], w2[t], phi1[t], phi2[t], ...};

Construct the model with all the states added to the outputs.

affinesys = NonlinearStateSpaceModel[equazioni, vars, motor[t], 
Join[{w[t] + phi[t]}, allVars], t]

Find the correct transformation that relates the old and new states.

trans = D[allVars /. 
 Solve[Rest[Normal[affinesys][[1, 2]]] == newNames, allVars], 
 newVars]

Transform the states so now they are ordered as in newNames.

affinesys = StateSpaceTransform[affinesys, trans]

Now do the renaming correctly.

affinesys = NonlinearStateSpaceModel[affinesys, newNames]

The outputs that were added to get the right transformation can now be deleted.

SystemsModelExtract[affinesys, {All, 1, All}]
Suba Thomas
  • 8,716
  • 1
  • 17
  • 32
  • Does this work if I have a set of ODES of different order? – Mirko Aveta Mar 13 '17 at 19:34
  • Kuba please add in your answer that the order in which the states happen to be in the list should be the same of that of the state variables appearing in the ODE set. – Mirko Aveta Mar 13 '17 at 19:49
  • 1
    The order does not matter. The idea is you can rename the states as you wish using NonlinearStateSpaceModel[..., states]. – Suba Thomas Mar 13 '17 at 19:51
  • I believe you are right! – Mirko Aveta Mar 13 '17 at 20:11
  • Suba please take a look at my update. – Mirko Aveta Mar 13 '17 at 20:53
  • 1
    I think I know what you are encountering. I will update my answer with a generic algorithm, but it will feel like groping one's way in dark because the actual equations are not there. Hopefully, you can take it from there. – Suba Thomas Mar 13 '17 at 21:30
  • Thanks @Suba. I'm attempting to first orderize the equations firstly. Please update your answer too. I can't upload the equations its takes 30 minutes only to load run them... – Mirko Aveta Mar 13 '17 at 21:32
  • My attempt did not work out :( – Mirko Aveta Mar 13 '17 at 21:54
  • Kuba trans returns a constant array of zeros. – Mirko Aveta Mar 13 '17 at 22:37
  • 1
    Mirko, I think Kuba is another user and I ignored your earlier comment to Kuba. So let me clarify the earlier comment. When you said 'order' I understood that as SystemsModelOrder, and that's what I meant when I said it does not matter. Your comment to Kuba about the 'order in which states happen' or the ordering is what we are grappling with here! – Suba Thomas Mar 14 '17 at 14:41
  • Of course, I expected you to adapt the code and not copy it verbatim, because it is pseudo-code. You have to thread the first argument of Solve over Equal and probably there are other minor tweaks too. – Suba Thomas Mar 14 '17 at 14:45