Number walls with mathematica

Question

I want to create "number walls" of a user-defined number of rows with mathematica. (They look similar to a CompleteKaryTree.)

Each pair of 2 values in a lower row adds up to a sum in the row above.
All numbers should be >0.

(1) How would you build up such a wall and (2) how can one remove randomly all "unnecessary" numbers so that the wall is still solvable?

Here is an example for a random wall consisting of 4 rows:

The solved wall is:

I started with the following code to create a wall:

makeWall[n_] := Module[{},
  data = RandomInteger[10, n];
  Print[data];
  l = Length@data;

  While[
   l > 1,
   data = Total[#] & /@ Partition[data, 2, 1];
   l = Length@data;
   Print[data];
   ];
  ]

SeedRandom[1];
makeWall[4]

{1,4,0,7}

{5,4,7}

{9,11}

{20}

How can be from a created wall a minimal number of wall values selected (in the example black), so that the wall can still be solved (red values)?

@Kuba: Each pair of 2 values in a lower row adds up to a sum in the row above. For 4 rows 4 starting numbers are sufficient to solve the wall, but they have to be placed properly. See: http://somos.crg4.com/nwic.html. I read this http://stackoverflow.com/questions/32681236/data-structure-for-number-wall and tried to rebuild the idea with mma, but was not successfull to find a general solution for the position of the starting values. — lio, Mar 19 '17 at 17:30
@Kuba: please excuse me for the misunderstanding, I added a sentence in the question. — lio, Mar 19 '17 at 17:34
@Kuba: Yes, the input would be the number of rows and the result should be any random solvable wall. — lio, Mar 19 '17 at 17:51
You probably should include the definition of 'solvable' too, and a requirement to return those positions, right? — Kuba, Mar 19 '17 at 17:55

swish · Accepted Answer · 2017-03-20T09:50:40.883

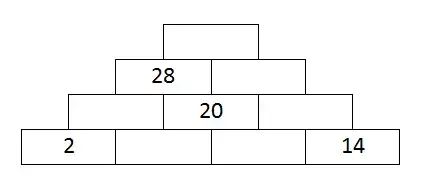
You can specify blanks with Null and construct the equations for Solve:

{{Null}, {28,}, {, 20,}, {2, , , 14}} /. Null :> Unique[];
% /. Solve[ListCorrelate[{1, 1}, #2] == #1 & @@@ Partition[%, 2, 1]]

(* {{{76}, {28, 48}, {8, 20, 28}, {2, 6, 14, 14}}} *)

EDIT

You can put maximum of n(n - 1)/2 blanks in order for wall to be uniquely (ok, sometimes, see below) solvable. This would construct a random wall with specified number of blanks with n(n - 1)/2 as default:

makeWall[n_, OptionsPattern[{Blanks -> n (n - 1)/2}]] := 
 Reverse@ReplacePart[#, 
     RandomSample[Position[#, _Integer], OptionValue[Blanks]] -> 
      Null] &@NestList[ListCorrelate[{1, 1}, #] &, 
   RandomInteger[10, n], n - 1]

And to wrap up the above solution:

solveWall = 
  With[{wall = # /. Null :> Unique[]}, 
    wall /. Solve[
      ListCorrelate[{1, 1}, #2] == #1 & @@@ Partition[wall, 2, 1], 
      Integers]] &;

Some examples:

makeWall[4]
solveWall@%

(*{{Null}, {18, 14}, {Null, 8, Null}, {3, Null, 1, Null}}*)
(*{{{32}, {18, 14}, {10, 8, 6}, {3, 7, 1, 5}}}*)

makeWall[5, Blanks -> 4]
solveWall@%

(*{{114}, {Null, 55}, {31, Null, 27}, {17, 14, Null, 13}, {10, Null, 7, 7, 6}}*)
(*{{{114}, {59, 55}, {31, 28, 27}, {17, 14, 14, 13}, {10, 7, 7, 7, 6}}}*)

Sometimes (depends on the positions of Nulls) there can be infinite number of solutions, parameterized with free variable C[1] to C[n(n+1)/2] (if you choose to fill the whole wall with Nulls):

makeWall[4]
solveWall@%

(*{{Null}, {14, Null}, {Null, Null, 14}, {Null, Null, 6, 8}}*)
(*{{{ConditionalExpression[C[1], C[1] \[Element] Integers]}, 
 {14, ConditionalExpression[-14 + C[1], C[1] \[Element] Integers]},
{ConditionalExpression[42 - C[1], C[1] \[Element] Integers], 
   ConditionalExpression[-28 + C[1], C[1] \[Element] Integers], 
   14}, 
{ConditionalExpression[76 - 2 C[1], C[1] \[Element] Integers],
    ConditionalExpression[-34 + C[1], C[1] \[Element] Integers], 6, 8}}}*)

You can pick possible values for these variables with:

% /. FindInstance[AllTrue[Flatten@%, # >= 0 &], C[1]]

(*{{{{35}, {14, 21}, {7, 7, 14}, {6, 1, 6, 8}}}, {{{37}, {14, 23}, {5, 
9, 14}, {2, 3, 6, 8}}}}*)

Thank you: please see my question ind the comment to Ali Hashmi. — lio, Mar 20 '17 at 08:33
@swish: Could you please help me once more. I adapted your solution and wrote a short code where I calculate 10 of unsolved and soved walls. Somehow the line /. FindInstance[AllTrue[Flatten@%, # >= 0 &], C[1]] does not the same as when I do it interactivly in a notebook with % /. .... Why does the following code not work: https://drive.google.com/open?id=0B9wKP6yNcpyfSVVfLTFKZ3JCUWM — lio, Mar 21 '17 at 10:54
@swish: which line has to be changed in the link file? You can download it. — lio, Mar 21 '17 at 12:19
@swish: What is the difference in the last two lines of this file? https://drive.google.com/open?id=0B9wKP6yNcpyfRjNCOWk2elRVbG8 (image of it: http://i.imgur.com/MRgMdcA.png) — lio, Mar 21 '17 at 13:29

Ali Hashmi · Answer 2 · 2017-03-20T15:35:42.203

3

Function to solve a wall with unknown parameters

solveWall[list_List] := With[{sym = Cases[list, _Symbol, {2}]},
FindInstance[#, sym, 
  Integers] &@(And @@ Map[x \[Function] First@x == Last@x, #] &@
  Flatten[Table[
    Thread[{Total /@ Partition[list[[i]], 2, 1], 
      list[[i + 1]]}], {i, 1, Length@list - 1}], 1])];

Borrowing the elegant approach from @swish except that I am using Symbol rather than Null.

makeWall[n_, OptionsPattern[{syms -> n (n - 1)/2}]] := With[
{base = RandomInteger[10, n]},
Module[{list}, 
list = NestList[Total /@ Partition[#, 2, 1] &, base, n - 1];
ReplacePart[list, Thread[RandomChoice[Position[list, _Integer],
OptionValue@syms] -> Table[Module[{x}, x], {OptionValue@syms}]]]
]]

test

wall = makeWall[4];
(* {{x$28197, 2, x$28202, 10}, {8, 7, x$28198}, {15, x$28200}, {37}} *)

wall /. First@solveWall[wall]
(* {{6, 2, 5, 10}, {8, 7, 15}, {15, 22}, {37}} *)

edited Mar 20 '17 at 15:35

answered Mar 19 '17 at 23:09

Ali Hashmi

8,950
4
22
42

Thank you: How would you find any possible starting list which can be solved, not only the one which I showed? – lio Mar 20 '17 at 08:28
1

@lio i will work on it today or tomorrow – Ali Hashmi Mar 20 '17 at 08:47
@ilo i added the makeWall which is a slightly modified version of the one provided by swish. It creates temporary symbols which is in spirit with my earlier answer – Ali Hashmi Mar 20 '17 at 17:05

Anjan Kumar · Answer 3 · 2017-03-20T00:02:18.883

3

Creating a random wall for a given number of rows.

  generateWall[n_] := Module[{vars, eqns, sol},
  vars = Table[Subscript[x, i, j], {i, n}, {j, i}];
  eqns = #1 + #3 == #2 & @@@ Partition[Riffle @@ Reverse[#], 3, 2] & /@
      Partition[vars, 2, 1] // Flatten;
  sol = FindInstance[Join @@ {eqns, Thread[Variables[vars] > 0]}, 
    Variables[vars], Integers];
  vars /. sol~Flatten~1]

For n = 5, we get

{{56}, {21, 35}, {8, 13, 22}, {3, 5, 8, 14}, {1, 2, 3, 5, 9}}

edited Mar 20 '17 at 00:02

answered Mar 19 '17 at 23:26

Anjan Kumar

4,979
1
15
28

I don't find much difference between my answer and the one you posted just now ! – Ali Hashmi Mar 19 '17 at 23:33
I was just trying to show another way of defining eqns. I don't know if this is accepted practice or not. If it is not, please let me know. – Anjan Kumar Mar 19 '17 at 23:34
@AnjanKumar since those are not exact duplicates you can just metion other posters for parts of your answer that really overlap with theirs. – Kuba Mar 20 '17 at 06:55
@AnjanKumar its fine by me. – Ali Hashmi Mar 20 '17 at 08:50
@AliHashmi Thank you for replying. I apologize for any inconvenience. – Anjan Kumar Mar 20 '17 at 09:36
@Kuba Thanks for your time and I apologize for any incovenience – Anjan Kumar Mar 20 '17 at 09:37
Thank you for your help. See also my follow up question: http://mathematica.stackexchange.com/questions/140525/fill-grid-with-list-data . – lio Mar 21 '17 at 15:44

Number walls with mathematica

3 Answers3