Ordered Subsequences of consecutive integers

Question

I have a list

  list={3, 4, 8, 1, 2, 5, 6, 7, 9}

and I want to find all the ordered subsequences of consecutive integers

in my example I should get

 {{3, 4}, {1, 2}, {5, 6, 7}}

as you can see {5,6}, {6,7} must NOT be included in the final result

score 10 · Accepted Answer · edited Apr 13 '17 at 12:55

10

Didn't find an exact duplicate so let's use another closely related:

How to detect if a sequence of integers is consecutive, credits to Simon Woods

consecutiveQ = Most[#] == Rest[#] - 1 &

SequenceCases[{3, 4, 8, 1, 2, 5, 6, 7, 9}, {_, __}?consecutiveQ]

{{3, 4}, {1, 2}, {5, 6, 7}}

edited Apr 13 '17 at 12:55

Community

1

answered Mar 19 '17 at 20:59

Kuba

136,707
13
279
740

thanx.it works! and it's elegant – ZaMoC Mar 19 '17 at 21:11
@Jenny Elegant, but unfortunately extremely slow on long lists. Please see my answer for a comparison. (My apologies Kuba for "attacking" your method.) – Mr.Wizard Jul 06 '17 at 07:05
@Mr.Wizard always feel free to do so as almost always I ignore performance in my answers. – Kuba Jul 06 '17 at 07:12

score 10 · Answer 2 · answered Mar 19 '17 at 21:10

10

Select[Split[list, #2 - #1 == 1 &], Length[#] > 1 &]

Also can get the same result

answered Mar 19 '17 at 21:10

yode

26,686
4
62
167

Can you modify this so that if you have a list like {1,2,3,5,7,8,9} you will get back {{1,2,3},{5},{7,8,9}} instead of {{1,2,3},{7,8,9}} ???? I am tempted to post the question but I thought I would ask first. – EGME Oct 11 '19 at 12:21
Ok, I figured out how to do this, you just set Length[#]>=1& ... – EGME Oct 11 '19 at 13:41

score 3 · Answer 3 · answered Jul 05 '17 at 16:30

Based on intervals from Find subsequences of consecutive integers inside a list:

consec[a_List] :=
  SparseArray[Differences@a, Automatic, 1]["AdjacencyLists"] //
    {a[[Prepend[# + 1, 1]]], a[[Append[#, -1]]]} & //
      Range @@@ Pick[#\[Transpose], Unitize[Subtract @@ #], 1] &

consec[{3, 4, 8, 1, 2, 5, 6, 7, 9}]

{{3, 4}, {1, 2}, {5, 6, 7}}

Benchmark including the two existing answers as fnK and fnY:

consecutiveQ = Most[#] == Rest[#] - 1 &;

fnK[lst_] := SequenceCases[lst, {_, __}?consecutiveQ]
fnY[lst_] := Select[Split[lst, #2 - #1 == 1 &], Length[#] > 1 &]

Needs["GeneralUtilities`"]

BenchmarkPlot[{fnK, fnY, consec}, RandomInteger[9, #] &, 2]

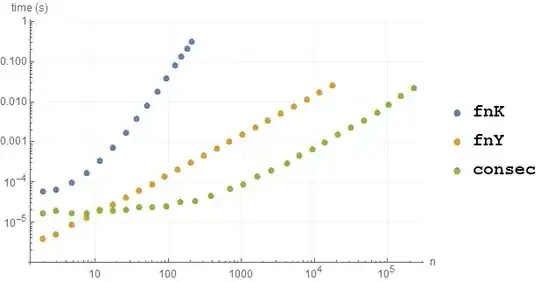
(Note the log-log scale.)

Ordered Subsequences of consecutive integers

3 Answers3

Linked