Clear[a]
seqHold = RecurrenceTable[{a[1] == Sqrt[2],
a[n + 1] == Sqrt[HoldForm[2 a[n]]]},
a[n], {n, 1, 5}]

The actual sequence is
seq = Map[ReleaseHold, seqHold, Infinity]
(* {Sqrt[2], 2^(3/4), 2^(7/8), 2^(15/16), 2^(31/32)} *)
Using FindSequenceFunction to determine the closed-form from this sequence
a1[n_] = 2^FindSequenceFunction[Log[2, seq], n] // Simplify
(* 2^(1 - 2^-n) *)
Alternatively, using RSolve to find the closed-form
a2[n_] = a[n] /. RSolve[
{a[1] == Sqrt[2], a[n + 1] == Sqrt[2 a[n]]},
a[n], n][[1]] // Simplify // Quiet
(* 2^(1 - 2^-n) *)
The two approaches are equivalent
a1[n] == a2[n]
(* True *)
EDIT: The limit of the sequence is
Limit[a2[n], n -> Infinity]
(* 2 *)
This can also be obtained using FixedPoint
FixedPoint[Sqrt[2 #] &, Sqrt[2.]]
(* 2. *)
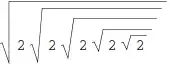


NestListrather thanNest– Bob Hanlon Mar 21 '17 at 23:48HoldForm[], useDefer[], so that the results can be copied, pasted, and executed without needing aReleaseHold[]. – J. M.'s missing motivation Mar 22 '17 at 02:10seq = NestList[Sqrt[2 #] &, Sqrt[2], 4], then2^FindSequenceFunction[Log[2, seq], n]and it worked. Then I tried using the Defer command, usingseq = NestList[Defer[Sqrt[2 #]] &, Sqrt[2], 4], then2^FindSequenceFunction[Log[2, seq], n], but this time it did not work. – David Mar 22 '17 at 16:07Defer[]prevents execution. Try this for yourself: runs = Defer[1 - 1]in a cell. In a new cell, runs. Then, copy the output cell of the first cell (which should be showing1 - 1), paste into a new cell, and run it. – J. M.'s missing motivation Mar 22 '17 at 16:35