FindPeaks confused by initial zeros?

Question

I think that there is something wrong with the FindPeaks algorithm. It seems to get confused when the data starts with some zeros. Here is works well:

Module[
    {data = N@Table[1 - Cos[x], {x, 0, 2 \[Pi], \[Pi]/100}]}, 
    ListPlot[data, Epilog -> {AbsolutePointSize[5], Red, Point /@ FindPeaks[data]}]]

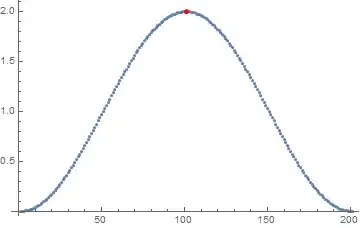
Now by adding some zeros, it fails to find this very simple peak:

Module[{data = N@Join[ Table[0, {32}], Table[1-Cos[x],{x,0,2 \[Pi], \[Pi]/100}]]},
    ListPlot[data, Epilog -> {AbsolutePointSize[5], Red, Point /@ FindPeaks[data]}]]

It not only fails to find the peak, it returns the lowest value (0) as a maximum!

Is this a bug? Is there a reliable way to avoid this behavior?

Additional, smaller examples:

In[1]:= FindPeaks[{0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0}]

Out[1]= {{9, 1}, {12, 1}}

In[2]:= FindPeaks[{0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0}]

Out[2]= {{9/2, 0}}

Update: This was reported back in 2017 to support as [CASE:3870515]. They acknowledged that "Mathematica could be doing a better job with automatic detection of peaks". I also provided a workaround function which support told me to continue use in the meanwhile:

autoFindPeaks[data_List, \[Sigma]_: Automatic] :=
    Module[{fp = FindPeaks[data, \[Sigma]], lowerPeakFound},
        lowerPeakFound = Min[Last /@ fp];
        Which[lowerPeakFound > Min[data],
              fp,
              fp == {} && Length[data] > 0 || lowerPeakFound == Min[data], 
              autoFindPeaks[data, If[\[Sigma] === Automatic, 0, \[Sigma] + 1]]]]

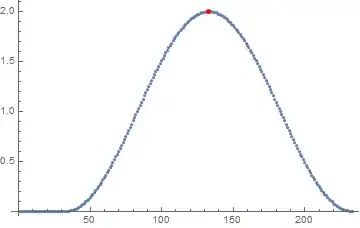
This function is not perfect, but it is better. It recursively increases the Gaussian smoothing for those cases when FindPeaks fails to produce results or when it returns an absolute minimum as a peak.

Module[{data = N@Join[ Table[0, {32}], Table[1-Cos[x],{x,0,2 \[Pi], \[Pi]/100}]]},
    ListPlot[data, Epilog -> {AbsolutePointSize[5], Red, Point /@ autoFindPeaks[data]}]]

The other way around is to use MATLAB's findpeaks via MATLink.