Numerical solution differential equations system in Excel and MMA

Question

In Excel I compiled some spreadsheets implementing the Runge Kutta method of the 4th order. Initially I tested with some systems of differential equations that are known to the analytical solution and the error was always the order of 10^-7 - 10^-5.

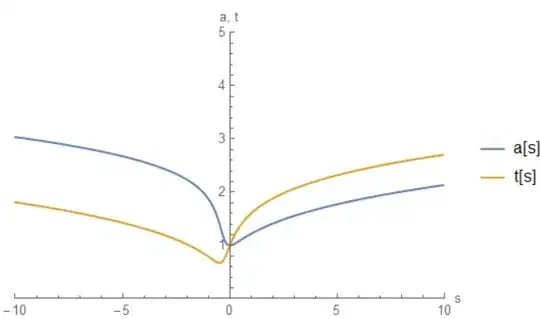
So I passed to the resolution of some of differentiable system of equations can not be solved analytically and the graphs obtained were perfectly coincident with those Wolfram Mathematica 11.0.1. It seemed to work wonders when all I had to face in the following system of differential equations:

ode1 = D[(a[s]^2 + 4a[s]^4t[s]^2)t'[s], s] - 4a[s]^4t[s]t'[s]^2 - 
         (a[s] + 8a[s]^3t[s]^2)a'[s]^2 == 0;

ode2 = D[4a[s]^2t[s]^4a'[s], s] - 4a[s]t[s]^4a'[s]^2 - 8a[s]^2t[s]^3t'[s]^2 == 0;

ic = {a[-10] == 3.03721, a'[-10] == -0.0555245, t[-10] == 1.81013, t'[-10] == -0.0608313};

sol = NDSolve[{ode1, ode2, ic}, {a, t}, {s, -10, 10}];

Plot[Evaluate[{a[s], t[s]} /. sol],
     {s, -10, 10},
     AxesLabel -> {"s", "a, t"},
     PlotLegends -> {"a[s]", "t[s]"},
     PlotRange -> {{-10, 10}, {0, 5}}]

or equivalently:

sol = NDSolve[
   {a'[s] == b[s],
    b'[s] == (-b[s]^2 t[s] - 4 a[s] b[s] u[s] + 2 a[s] u[s]^2)/(a[s] t[s]),
    t'[s] == u[s],
    u'[s] == (b[s]^2 + 8 a[s]^2 b[s]^2 t[s]^2 - 2 b[s] u[s] - 16 a[s]^2 b[s] t[s]^2 u[s] - 
              4 a[s]^3 t[s] u[s]^2)/(a[s] (1 + 4 a[s]^2 t[s]^2)),
    a[-10] == 3.03721,
    b[-10] == -0.0555245,
    t[-10] == 1.81013,
    u[-10] == -0.0608313},
   {a, b, t, u}, {s, -10, 10}];

Plot[Evaluate[{a[s], t[s]} /. sol],
     {s, -10, 10},
     AxesLabel -> {"s", "a, t"},
     PlotLegends -> {"a[s]", "t[s]"},
     PlotRange -> {{-10, 10}, {0, 5}}]

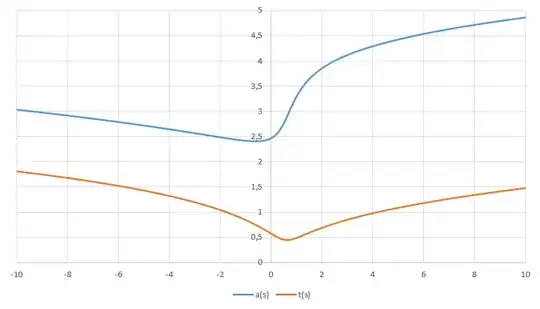
while in Microsoft Excel 2016 I get the following graph:

You might point out some strategies to check the accuracy of such graphs? How do you be certain of the graphs obtained from MMA without the possibility of an analytical feedback? It may be that there are numeric problems?

Thanks so much!