1

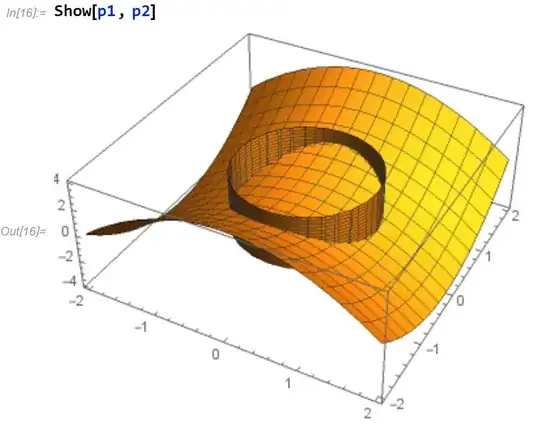
I'm trying to find the graphic of the curve of the intersection of the hyperbolic paraboloid $z=y^2-x^2$ and the cylinder $x^2+y^2=1$. I could show them together:

I want to see the curve of intersection highlighted, is it possible? I've already searched everywhere without success.

user26832
  • 141
  • 5
  • Have you seen this? – J. M.'s missing motivation Mar 30 '17 at 13:27
  • @J.M. Thank you very much. I followed one of the answers and plot: ContourPlot3D[{x^2 + y^2 == 1, z=y^2-x^2}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2},Contours -> {0}, ContourStyle -> Opacity[0], Mesh -> None, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Green, Tube[.03]}}}, Boxed -> False]. Mathematica tells me y^2-x^2 is not a valid variable – user26832 Mar 30 '17 at 13:38
  • Clear all variables (ClearAll["Global`*"]) and try again. Also, your second equation should be z == y^2 - x^2; = and == are different things. – J. M.'s missing motivation Mar 30 '17 at 13:40
  • @J.M. Thank you again, it worked. However I couldn't put them together, Mathematica says: Show :Could not combine the graphics objects in Showp1,p2, .

    General :Further output of Get::noopen will be suppressed during this calculation.

    Get :Cannot open 1241>> .

    Get :Cannot open 1241>> .

    Get :Cannot open 1>> .

     – user26832 Mar 30 '17 at 13:45
  • @J.M. I put Show[p1,p2,p3], where p1=Plot3D[z=y^2-x^2,{x,-2,2},{y,-2,2}], p2=ContourPlot3D[x^2 + y^2 == 1, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}],p3=ContourPlot3D[{x^2 + y^2 == 1, z==y^2-x^2}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2},Contours -> {0}, ContourStyle -> Opacity[0], Mesh -> None, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Green, Tube[.03]}}}, Boxed -> False] – user26832 Mar 30 '17 at 13:46
  • Try removing the ContourStyle -> Opacity[0] in the code you have. Also, you have again made the mistake of using = in p1; it is not necessary there. Please do be careful about this. – J. M.'s missing motivation Mar 30 '17 at 13:46
  • It worked when I write p3=ContourPlot3D[{x^2 + y^2 == 1, z==y^2-x^2}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2},Contours -> {0}, Mesh -> None, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Green, Tube[.03]}}}, Boxed -> False]. Thank you very much. However the show command still have the same problems – user26832 Mar 30 '17 at 13:50
  • @J.M. When I wrote: p1=Plot3D[z==y^2-x^2,{x,-2,2},{y,-2,2}], this gave me an empty box. Did you know why? – user26832 Mar 30 '17 at 14:02
  • You don't need the z== in Plot3D[], as you can see from the documentation. Also, the ContourPlot3D[] without the ContourStyle -> Opacity[0] should already be showing the two surfaces, so I don't understand why you insist on using Show[]. – J. M.'s missing motivation Mar 30 '17 at 14:04
  • I've just made a commentary, it's already worked with ContourPlot3D. Thank you again! you helped me a lot. – user26832 Mar 30 '17 at 14:10

0 Answers0