4

I am attempting to calculate the mean curvature [1, 2] of a surface defined by a function of x and y.

My function is rather simple:

f = 1 - 0.05(Cos[2 π x/L] + Sin[2 π x/L])Cos[2 π y/L];

So to calculate the mean curvature, this is what I do (κ is the mean curvature below):

L=79.1829;
f = 1 - 0.05(Cos[2 π x/L] + Sin[2 π x/L])Cos[2 π y/L];
κ=((1 + D[f,x]^2) D[f,y,y]-2 D[f,x]D[f,y]D[D[f,x],y]+
  (1+D[f,y]^2)D[f,x,x])/((1 + D[f,x]^2 + D[f,y]^2)^1.5)

And then I plot it as :

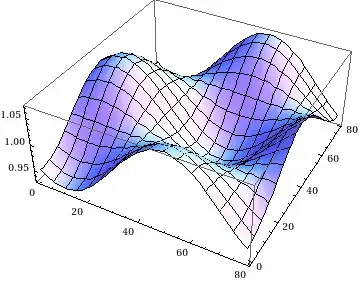
(*Surface defined by f*)
Plot3D[
  f,
  {x, 0, L},
  {y, 0, L}
  ]

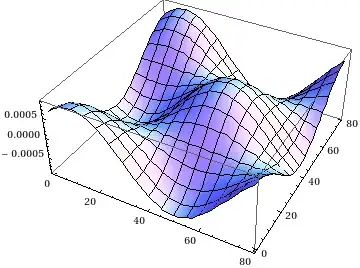
enter image description here

 (*Plot of kappa*)
 Plot3D[
  κ,
  {x, 0, L},
  {y, 0, L}
  ]

enter image description here

  1. I wasn't entirely sure of whether to post this question in math.se or mathematica.se but I did so on mathematica.se since it does have a Mathematica component to it.

  2. Is what I am doing correct? I ask because this seems rather trivial.

  3. Does anyone have any suggestion as to do this in a better way, perhaps plot it in a better way?

A little background:

I am trying to prove quantitatively that different initial conditions created by the surface like f would engender different amounts of curvature for a fluid dynamics problem.

Michael E2
  • 235,386
  • 17
  • 334
  • 747
dearN
  • 5,341
  • 3
  • 35
  • 74
  • 1
    Read thoroughly e.g. : http://mathematica.stackexchange.com/questions/8895/how-to-calculate-scalar-curvature-ricci-tensor-and-christoffel-symbols-in-mathem – Artes Nov 05 '12 at 14:32
  • 1
    That's a surface, not a curve... anyway, I gave a routine for the mean curvature here. – J. M.'s missing motivation Nov 05 '12 at 14:34
  • @Artes I actually did. Doesn't seem to be the same thing. It does have certain functions that would be interesting though. – dearN Nov 05 '12 at 14:34
  • @J.M. Oops! Will make the edit! – dearN Nov 05 '12 at 14:35
  • 1
    A great way to test formulas or code involving curvature is to apply it to objects with known curvature. In this case, when you compute the mean curvature function for a unit sphere you get a constant value of $2$, which is correct. Good test objects (in 3D) for mean curvatures include spheres (of various sizes), any soap bubble (which should have zero mean curvature everywhere), tori, ruled surfaces, and surfaces of revolution. – whuber Nov 05 '12 at 16:19
  • @J.M. why don't you migrate that answer here? Its a mathematica answer isn't it? – chris Nov 05 '12 at 16:25
  • @chris, there's still the (admittedly remote) possibility that somebody might contribute a MATLAB answer, which would be fine there, but not here. – J. M.'s missing motivation Nov 05 '12 at 16:38
  • @whuber +1! I'll do that. Calculate the curvature of a unit sphere. – dearN Nov 05 '12 at 18:05

0 Answers0