5

I am learning precision and accuracy in Mathematica numerics. I need little help to try to understand why I am not getting the same result I expect in the following. I have 2 numbers, each is 50 decimal point and differ by the 50'th decimal point.

So when I take the difference, I expected to get 1/10000....0000 with 50 zeros there. I did make sure the numbers are entered using SetPrecision[...,Infinity]

So I must be doing something wrong. Or not doing something in addition to this. There are so many options related to accuracy and precision in Mathematica, and it can get confusing for me what to set and to what value. Here is the code

r0=SetPrecision[0.12345678901234567890123456789012345678901234567890,Infinity];
r1=SetPrecision[0.12345678901234567890123456789012345678901234567891,Infinity]; 

r1-r0

Mathematica graphics

(I also tried SetPrecision[r1-r0,Infinity], no difference)

The equivalant Maple code is 

Digits:=100: #for display
r0:=0.12345678901234567890123456789012345678901234567890:
r1:=0.12345678901234567890123456789012345678901234567891:
r1-r0;

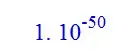
Mathematica graphics

convert(r1-r0,rational,'exact');

Mathematica graphics

Question is: How can one obtain the same result as shown in Maple output?

I am using 11.1 on windows 7.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Nasser
  • 143,286
  • 11
  • 154
  • 359
  • must you use SetPrecision? – bobbym Apr 02 '17 at 07:40
  • @bobbym well, I was just told to do so here http://mathematica.stackexchange.com/questions/141604/how-to-get-exact-rationalize-of-a-decimal-number That is what so confusing about all of this. – Nasser Apr 02 '17 at 07:42
  • Check this: http://mathematica.stackexchange.com/questions/135636/understanding-simple-numerical-calculation – Anjan Kumar Apr 02 '17 at 07:51
  • @AnjanKumar thanks. But the above is all about floating point stuff. I want to do symbolic stuff. Just like on piece of paper. That is what I am using Mathematica and not Matlab :) On paper, I should get same result shown by Maple (another computer algebra program). That is why I set precision to infinity. I want exact decimal point calculations, like on paper. – Nasser Apr 02 '17 at 08:01
  • @Nasser, but Maple gave a floating point answer, which then had to be converted to an exact one. – bobbym Apr 02 '17 at 08:21
  • @bobbym maple uses decimal point representation internally, not hardward floating point. The numbers are still exact internally as you can see. The actual output of 1*10^-50 vs fraction is not important, as I can convert from to the another. This is just display issue. Maple can do hardware floating point if needed. But default is decimal point. – Nasser Apr 02 '17 at 08:29

2 Answers2

5

Since you want decimal representation:

dec = # ~RealDigits~ 10 ~FromDigits~ 10 &;

r0 = 0.12345678901234567890123456789012345678901234567890;
r1 = 0.12345678901234567890123456789012345678901234567891;

dec[r1] - dec[r0]

1/100000000000000000000000000000000000000000000000000

Of course the default is decimal so this can be written less explicitly as:

dec = FromDigits @* RealDigits;

Related:

Community
  • 1
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 1
    There somehow exists an edge case for 17 digits long real numbers, where an implicit conversion to MachinePrecision happens that can remove the last digit. For example one has to use something like r0 = 0.12345678901234567`17; r1 = 0.12345678901234568`17; instead of r0 = 0.12345678901234567; r1 = 0.12345678901234568; to get dec[r1] - dec[r0] not returning 0. – Karsten7 Apr 02 '17 at 08:40
  • @Karsten7 Thanks for the note! – Mr.Wizard Apr 02 '17 at 08:46
3

If you just want to duplicate Maple's answer.

r0 = 0.12345678901234567890123456789012345678901234567890000000000;
r1 = 0.12345678901234567890123456789012345678901234567891000000000;

r1 - r0

(*1.00000000*10^-50*)
bobbym
  • 2,628
  • 2
  • 15
  • 20
  • Thanks, but I do not understand why you had to add more zeros there? I'd like to duplicate the answer given the input as is. What is the reason to modify the input and adding arbitrary zeros? And I thought one is supposed to use SetPrecision when entering decimals numbers with lots of digits. – Nasser Apr 02 '17 at 07:48
  • I did not mean to confuse you, I agree with your complaints. The adding of zeroes tells mathematica that the error in the numbers is less. Trailing zeroes are significant when there is a decimal point. You can take a look at your last post where in my answer I used the same trick. – bobbym Apr 02 '17 at 07:52