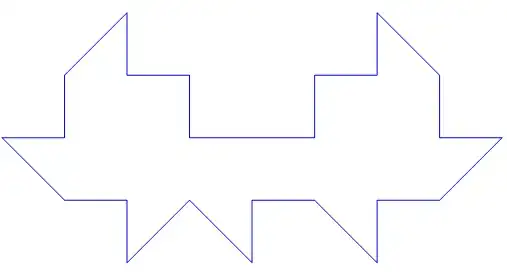
Art Gallery Theorem. If the walls of an art gallery are made up of $n$ straight line segments, then the entire gallery can always be supervised by $\lfloor{\frac{n}{3}}\rfloor$ watchmen placed in corners.
How can I find $\lfloor{\frac{24}{3}}\rfloor=8$ points (corners) in the Castro's room according the Art Gallery Theorem?
Castro24 = {{1, 0}, {1, 1}, {2, 1}, {2, 2}, {3, 1}, {3, 0}, {4, 0}, {3, -1},
{3, -1}, {2, -1}, {2, -2}, {1, -1}, {0, -1}, {0,-2}, {-1, -1}, {-2, -2},{-2, -1},
{-3, -1}, {-4, 0}, {-3, 0}, {-3, 1}, {-2, 2}, {-2, 1}, {-1, 1}, {-1, 0}, {1, 0}};
Graphics[{Blue, Line[First[#]]} & /@ {{Castro24}}]
Thank you in advance to any one who may be able to give me some ideas
RegionWithinis buggy. I getTrueforRegionWithin[Polygon[Castro24], Line[{Castro24[[{19, 21}]]}]]but look atGraphics[{LightBlue, Polygon[Castro24], Red, Line[{Castro24[[{19, 21}]]}]}]. Am I missing something? – Szabolcs Apr 03 '17 at 09:52