Finding C[i]'s expression in DSolve solution

Question

An example, the command

DSolve[y''[x] - 4 y[x] == 1, y[x], x]

gives solution

y[x] -> -(1/4) + E^(2 x) C[1] + E^(-2 x) C[2]

The same command with initial conditions

DSolve[{y''[x] - 4 y[x] == 1, y[0] == 1, y'[1] == -1}, y[x], x]

gives solution

y[x] -> -((E^(-2 x) (-2 E^2 - 5 E^4 + E^(2 x) - 5 E^(4 x) + E^(4 + 2 x) + 
2 E^(2 + 4 x)))/(4 (1 + E^4)))

In the first case, the solution has very clear structure: an increasing component, a decreasing component, and a particular solution. In the second case, this structure is shadowed by the complicated expression. Here is a picture of the commands & results in Mathematica:

I think most people would prefer the 2nd solution to be presented in similar form as in the first case. Something like:

The solution is $y = c_1 h_1(x) + c_2 h_2(x) + g(x)$, in which $h_1(x) = e^{2 x}$ is the first homogeneous solution, $h_2(x) = e^{-2 x}$ is the second homogeneous solution, and $g(x)=-1/4$ is the particular solution. The coefficients $c_1, c_2$ are determined from initial conditions. In this particular case we have $ c_1 = ; c_2 = $.

Is there a way to extract $c_1$ and $c_2$? Pattern matching might work in this simple example, but I don't think it generalizes to more complicated cases.

xzczd · Accepted Answer · 2017-04-05T04:02:02.210

It's possible to dig out C[_] directly from DSolve, with the help of TraceInternal:

eqn = y''[x] - 4 y[x] == 1;

constant = 
 Trace[DSolve[{eqn, y[0] == 1, y'[1] == -1}, y[x], x], HoldPattern[C[_] -> _], 
      TraceInternal -> True] // Flatten // ReleaseHold // Simplify // Union
(* {C[1] -> (5 - 2 E^2)/(4 + 4 E^4), C[2] -> (2 E^2 + 5 E^4)/(4 + 4 E^4)} *)

Or a bit shorter:

constant = Trace[DSolve[{eqn, y[0] == 1, y'[1] == -1}, y[x], x], 
    HoldPattern[{(C[_] -> _) ..}], TraceInternal -> True] // ReleaseHold // Flatten

score 6 · Answer 2 · answered Apr 04 '17 at 20:02

The most obvious answer is to solve for the constants from the general solution directly. In this example, let

gensol = DSolve[y''[x] - 4 y[x] == 1, y[x], x][[1, 1, 2]]
(*-(1/4) + E^(2 x) C[1] + E^(-2 x) C[2]*)

Now we can construct a system of equations based on the boundary conditions specified in the problem to get explicit values for our general solution constants.

FullSimplify@
 Solve[{Evaluate[gensol /. x -> 0] == 1, 
   Evaluate[D[gensol, x] /. x -> 1] == -1}, {C[1], C[2]}]
(*{{C[1] -> (5 - 2 E^2)/(4 + 4 E^4), 
  C[2] -> (2 E^2 + 5 E^4)/(4 + 4 E^4)}}*)

In this example we also mess around a bit with the full solution to extract the general solution constants.

totsol = DSolve[{y''[x] - 4 y[x] == 1, y[0] == 1, y'[1] == -1}, y[x], 
   x][[1, 1, 2]]
(*-((E^(-2 x) (-2 E^2 - 5 E^4 + E^(2 x) - 5 E^(4 x) + E^(4 + 2 x) + 
    2 E^(2 + 4 x)))/(4 (1 + E^4)))*)

Collecting the results based on one of the functions appearing in the general solution we can extract the constants.

Collect[Expand[totsol], E^(2 x)]
(*-(1/(4 (1 + E^4))) - E^4/(4 (1 + E^4)) + 
 E^(2 x) (5/(4 (1 + E^4)) - E^2/(2 (1 + E^4))) + 
 E^(-2 x) (E^2/(2 (1 + E^4)) + (5 E^4)/(4 (1 + E^4)))*)

We can now simplify things a bit to get the constants.

FullSimplify[-(1/(4 (1 + E^4))) - E^4/(4 (1 + E^4))]
(*-(1/4)*)
FullSimplify[{(5/(4 (1 + E^4)) - E^2/(2 (1 + E^4))), (E^2/(
    2 (1 + E^4)) + (5 E^4)/(4 (1 + E^4)))}]
(*{(5 - 2 E^2)/(4 + 4 E^4), (2 E^2 + 5 E^4)/(4 + 4 E^4)}*)

Checking that we get the same answer in both methods:

FullSimplify[{(5/(4 (1 + E^4)) - E^2/(2 (1 + E^4))), (E^2/(
     2 (1 + E^4)) + (5 E^4)/(4 (1 + E^4)))}] == 
 Flatten@FullSimplify@
   Solve[{Evaluate[gensol /. x -> 0] == 1, 
      Evaluate[D[gensol, x] /. x -> 1] == -1}, {C[1], 
      C[2]}][[;; , ;; , 2]]
(*True*)

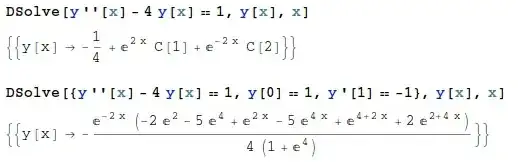
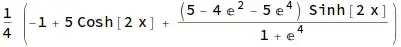
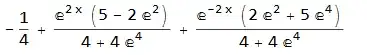
Same idea, slightly different functions/usage: foo = Collect[Expand[totsol], E^(2 x), Simplify], Simplify@Coefficient[foo, {E^(2 x), E^(-2 x)}], Coefficient[foo, {E^(2 x)}, 0] — Michael E2, Apr 04 '17 at 20:30
Actually Evaluate isn't necessary, you can simply use parentheses or e.g. gensol == 1 /. x -> 0 — xzczd, Apr 05 '17 at 07:26

Akku14 · Answer 3 · 2017-04-05T06:44:11.617

4

If you do it the following way, applying the shown rules, you get the desired result.

This can be used for all types of equations.

    dsol = First@DSolve[y''[x] - 4 y[x] == 1, y, x]

    (*   {y -> Function[{x}, -(1/4) + E^(2 x) C[1] + E^(-2 x) C[2]]}    *)

    sol = First@Solve[{y[0] == a, y'[0] == b} /. dsol, {C[1], C[2]}]

    (*    {C[1] -> 1/8 (1 + 4 a + 2 b), C[2] -> 1/8 + a/2 - b/4}    *)

    ys[x_, a_, b_] = (y[x] /. dsol /. sol)

    (*   -(1/4) + (1/8 + a/2 - b/4) E^(-2 x) + 1/8 (1 + 4 a + 2 b) E^(2 x)   *)

edited Apr 05 '17 at 06:44

answered Apr 05 '17 at 06:01

Akku14

17,287
14
32

@ xzczd you are right. You get the same effect without Unevaluated. Then this is the solution without Unevaluated. – Akku14 Apr 05 '17 at 06:40

score 3 · Answer 4 · answered Apr 04 '17 at 20:35

Once defined the following function:

dsolve[ode_, ic_, fun_, var_] :=
  Module[{constant, i},
     fun = DSolve[ode, fun, var][[1, 1, 2]];
     constant = Table[C[i], {i, 1, Length[ic]}];
     constant = Solve[ic, constant];
     For[i = 1, i <= Length[ic], i++,
         fun = fun /. C[i] -> constant[[1, i, 2]]
        ];
  Return[fun[[2]]]];

writing:

Clear[y]
ode = y''[x] - 4 y[x] == 1;
ic = {y[0] == 1, y'[1] == -1};
dsolve[ode, ic, y, x]

you get:

-(1/4) - (E^(2 x) (-5 + 2 E^2))/(4 (1 + E^4)) - (E^(-2 x) (-2 E^2 - 5 E^4))/(4 (1 + E^4))

which is as much as desired.

I'm sorry, but this function isn't that… good. Let alone the redundant Return and unnecessary For, the most serious issue is, fun will be polluted. Just try executing dsolve[ode, ic, y, x] twice. A possible countermeasure is to introduce another intermediate variable in Module. — xzczd, Apr 05 '17 at 08:24

score 3 · Answer 5 · answered Apr 04 '17 at 20:37

SolveAlways cannot handle the mixed forms E^(2 + 4 x), E^(4 x), etc., but a change of variables fixes that.

gensol  = First@DSolve[y''[x] - 4 y[x] == 1, y[x], x];
partsol = First@DSolve[{y''[x] - 4 y[x] == 1, y[0] == 1, y'[1] == -1}, y[x], x];

SolveAlways[(y[x] /. gensol) == (y[x] /. partsol) /. x -> Log@u, u]
(*
  {{C[1] -> (5 - 2 E^2)/(4 (1 + E^4)), 
    C[2] -> (2 E^2 + 5 E^4)/(4 (1 + E^4))}}
*)

score 3 · Answer 6 · answered Apr 04 '17 at 23:20

3

This works:

DSolve[{y''[x] - 4 y[x] == 1, y[0] == 1, y'[1] == -1}, y[x], x] // 
 Collect[#, E^(2 x)] &

answered Apr 04 '17 at 23:20

corey979

23,947
7
58
101

score 3 · Answer 7 · answered Apr 05 '17 at 03:10

3

Another form with a compact structure is

soln = First@DSolve[
     {y''[x] - 4 y[x] == 1, y[0] == 1, y'[1] == -1}, y[x], x];

soln // ExpToTrig // FullSimplify

answered Apr 05 '17 at 03:10

LouisB

12,528
1
21
31

zhk · Answer 8 · 2017-04-05T07:21:34.220

3

Here is another way to find C's

eqn = y''[x] - 4 y[x] == 1;
s = DSolve[eqn, y[x], x];
gsol[x_] = y[x] /. Flatten[s];
dgsol[x_] = D[y[x] /. Flatten[s], x];
findCs = Solve[{gsol[0] == 1, dgsol[1] == -1}, {C[1], C[2]}]// Simplify

gsol[x] /. Flatten[findCs]

Simplify[eqn /. {{y[x] -> %}} /. {{y''[x] -> D[%, x, x]}}]

{{True}}

edited Apr 05 '17 at 07:21

answered Apr 05 '17 at 07:10

zhk

11,939
1
22
38

Finding C[i]'s expression in DSolve solution

8 Answers8