Backslide introduced in 11.1, fixed in 11.2.
In Mathematica 11.0, the following limit,
Limit[Power[Sqrt[((1 - 4 n)/(3 n + 2))^(3 n)]^2, (n)^-1], n -> ∞]
gave me an answer of $e^{6 \operatorname{arctanh}(1/7)}$, which equals 64/27, but in Mathematica 11.1, it doesn't give an answer. Anyone else experience this problem?
Granted, with Mathematica 11.1.0, this does work:
Limit[Power[RealAbs[((1 - 4 n)/(3 n + 2))^(3 n)], (n)^-1], n -> ∞]
Giving a correct answer of 64/27.
Update: Due to Anjan Kumer's suggestion, I tried:
Limit[Power[Sqrt[((1 - 4 n)/(3 n + 2))^(3 n)]^2, (n)^-1],
n -> \[Infinity]] // PowerExpand
But it gave an incorrect answer of $-64/27$.
Update #2: I believe there has been some editing to my question. This question arises when we are using the Root Theorem in calculus, which requires that we investigate $$\lim_{n\to\infty}\sqrt[n]{|a_n|}$$ in order to determine if the series $\sum_{n=1}^{\infty}a_n$ converges. Due to difficulties with Mathematica's Abs command over the years, and the fact that $\sqrt{x^2}=|x|$, we frequently use this fact to avoid difficulties. Thus, using the Root Test to determine the convergence of the series $$\sum_{n=1}^{\infty}\left(\frac{1-4n}{3n+2}\right)^{3n}$$ requires that we evaluate the limit: $$\lim_{n\to\infty}\sqrt[n]{\left|\left(\frac{1-4n}{3n+2}\right)^{3n}\right|}$$ Now, I made a mistake and used the absolute value bars in the Writing Assistant in my input. Now, I note that the following works and gives the correct answer (I am copying and pasting an image of my input and output).
Now, notice what happens when I try to use the fact that $\sqrt{x^2}=|x|$ (Again, I am copying and pasting an image of my input and output).
See, the exponent 2 is inside the Sqrt brackets, not outside. However, again a different answer.
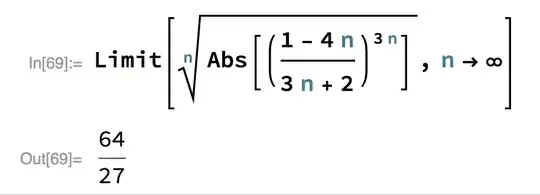
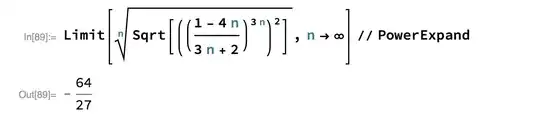

PowerExpand. – Anjan Kumar Apr 06 '17 at 07:17