ColorFunction -> Hue not respected?

Question

I am encountering a bizarre problem. I'm trying to generate the complex phase plot of the (principal branch of) the square root function by using DensityPlot on the argument of the square root with ColorFunction -> Hue.

Arg[Sqrt[-1]]

gives $\pi/2$ as expected. Then

Hue[Rescale[Arg[Sqrt[-1]], {-π, π}]]

gives .

However,

DensityPlot[
      Rescale[Arg[Sqrt[x + I y]], {-π, π}], {x, -1, 1}, {y, -1, 1},
      PlotPoints -> 100, ColorFunction -> Hue, Exclusions -> None]

produces

which is clearly painting $-1$ in red.

Is this a bug?

Try ColorFunctionScaling -> False. Usually Mathematica rescales your values to (0, 1). — b3m2a1, Apr 06 '17 at 23:11

score 4 · Accepted Answer · edited Apr 13 '17 at 12:56

4

First, let's look at what $\arg$ looks like in Mathematica:

Plot3D[Arg[x + I y], {x, -4, 4}, {y, -4, 4}]

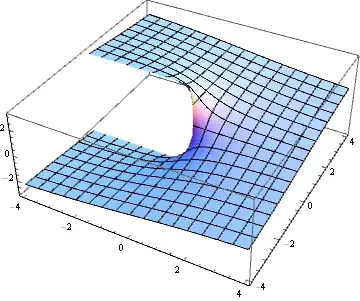
phase of a complex number

Note that $\arg$'s codomain here is $(-\pi,\pi]$, and that the branch cut runs along the ray $(-\infty,0)$. Thus, when you use Rescale[x, {-π, π}], values along the negative real axis ($\arg z=\pi$) get mapped to 1, and Hue[1] is of course a nice shade of red.

In this case, you'll want a preliminary application of $\bmod$ to $\arg$, to get results on the interval $[0,2\pi)$ and see the expected color wheel:

DensityPlot[Mod[Arg[x + I y], 2 π], {x, -1, 1}, {y, -1, 1}, ColorFunction -> Hue,
            Exclusions -> None, PlotPoints -> 100]

complex color wheel

Note the conspicuous lack of a Rescale[]. This is due to the setting ColorFunctionScaling being set to True by default, which rescales the values of the function before they are fed to the ColorFunction; thus, Hue[] is only seeing values in $[0,1]$. If you set ColorFunctionScaling -> False, then you do need an explicit Rescale[]:

DensityPlot[Rescale[Mod[Arg[x + I y], 2 π], {0, 2 π}], {x, -1, 1}, {y, -1, 1},
            ColorFunction -> Hue, ColorFunctionScaling -> False,
            Exclusions -> None, PlotPoints -> 100]

which should yield the very same color wheel.

Finally, here is what $\sqrt{z}$ looks like when "domain colored":

DensityPlot[Mod[Arg[Sqrt[x + I y]], 2 π], {x, -1, 1}, {y, -1, 1}, 
            ColorFunction -> Hue, Exclusions -> None, PlotPoints -> 100]

domain coloring of the square root function

Last, but not the least, this previous thread on domain coloring might be of interest.

edited Apr 13 '17 at 12:56

Community

1

answered Apr 06 '17 at 23:22

J. M.'s missing motivation

124,525
11
401
574

For interest's sake here is what the above looks like when colored with a cyclic isoluminant colormap. – Quantum_Oli Apr 07 '17 at 10:12
@Quantum, which of the color maps in that page did you use? I see entries for cyclic colormaps, and entries for isoluminant colormaps, but nothing with both properties. – J. M.'s missing motivation Apr 07 '17 at 10:16
Sorry, that was misleading! It's not from that page, but its properties are well-described on that page. The map I've used is a line cut (at lightness 0.78) from the 2D map shown in this question. It just shows how with an isoluminant map the apparent lines, especially in the yellow and pink, disappear. – Quantum_Oli Apr 07 '17 at 10:26
Yes, that's why I was interested in your colormap; would you consider writing a Q&A on this, then? – J. M.'s missing motivation Apr 07 '17 at 10:35
Thanks for this answer. I find that unless I use an explicit Rescale and set ColorFunctionScaling->False, it fails for the constant function whose value is i. – José Figueroa-O'Farrill Apr 07 '17 at 12:38
@José, yes, DensityPlot[] does not really work too well for functions that are "flat" or nearly so, I've found. – J. M.'s missing motivation Apr 07 '17 at 12:58

ColorFunction -> Hue not respected?

1 Answers1