I am ploting electronic band structure in Mathematica using ListLinePlot. Like this
However I don't want those vertical Lines indicated by red circle.
I want to delete those vertical lines and get this feel
An idea maybe to post-process the plot and keep styles intact. But I got lost in the complicated FullForm of Plot.
A simple example to start is for example ListLinePlot[{{1, 1}, {2, 1}, {2, 2}, {3, 2}}, Frame -> True]


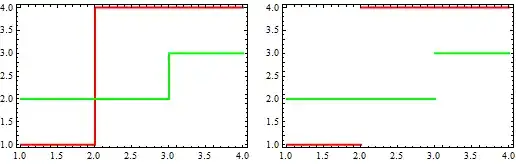
ListLinePlot[ Split[{{1, 1}, {2, 1}, {2, 2}, {3, 2}}, First[#] != First[#2] &], Frame -> True]? – kglr Apr 11 '17 at 11:52ListLinePlot. – Michael E2 Apr 11 '17 at 11:53ListLinePlot[{{1, 1}, {2, 1}, {2, 2}, {3, 2}}, Frame -> True] /. Line[x_] :> (Line /@ Split[x, First[#] != First[#2] &])– kglr Apr 11 '17 at 14:03Splitcriterion to the scale of the data as necessary (e.g. change< 10to< 0.1, or perhaps using the slope & bounding box of the data for the criterion). @kglr used the same approach as Mr.Wizard (post-processing withSplit), but my thought was that what criterion works depends on the data and what should count as a gap. – Michael E2 Apr 12 '17 at 11:02