Filling a ListPlot with an optical spectrum

Question

I have discrete optical spectra data consisting of pairs of wavelengths and intensities, and I would like to make a ListPlot in which the points are both joined, and colored according to the wavelength as is the filling.

Here is an example.

Here's fake data that illustrates the problem:

ListPlot[
 Table[Style[{λ, Sin[λ/400]}, 
   ColorData["VisibleSpectrum"][λ]],
   {λ, 400, 700, 5}], 
 PlotStyle -> PointSize[Medium],
 Filling -> Axis,
 FillingStyle -> Function[{λ, y}, ColorData["VisibleSpectrum"][#[[1]] &]]]

I can get the points to be properly colored, but not the filling. Moreover, the ideal is to have a continuous filling underneath curve (as in the linked example), i.e., not discrete bars. I've tried numerous variations on the FillingStyle, without success.

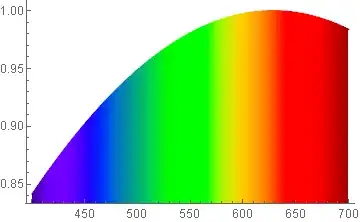
You might want to use the color functions here instead of ColorData["VisibleSpectrum"]. — J. M.'s missing motivation, Apr 18 '17 at 01:28
But VisibleSpectrum takes the wavelength (in nanometers) and renders the color—just as is the form of my data. Shouldn't there be an easy way to call VisibleSpectrum in FillingStyle?! — David G. Stork, Apr 18 '17 at 01:32
My point in making my earlier comment was that "VisibleSpectrum" does not always give accurate colors. It was only a suggestion; if you insist on using "VisibleSpectrum", then sure, you can use it in FillingStyle: ListLinePlot[Table[{x, Sin[x/400]}, {x, 400, 700, 5}], ColorFunction -> (ColorData["VisibleSpectrum", #] &), ColorFunctionScaling -> False, Filling -> Axis] — J. M.'s missing motivation, Apr 18 '17 at 01:34

bill s · Accepted Answer · 2017-04-18T01:48:57.750

5

fcolor = ColorData["VisibleSpectrum"]; 
ListPlot[Table[{x, Sin[x/400]}, {x, 400, 700, 5}], Joined -> True, 
 ColorFunction -> Function[{x, y}, fcolor[x]], 
 ColorFunctionScaling -> False, Filling -> Axis]

edited Apr 18 '17 at 01:48

answered Apr 18 '17 at 01:15

bill s

68,936
4
101
191

Almost. I had found such a ColorFunction but 1) the color should be a function of the abscissa ($x$) value (not $y$ value) and 2) it should be colored according to ColorData["VisibleSpectrum"] (not Hue). Any way to fix that in your code? (I couldn't find it.) – David G. Stork Apr 18 '17 at 01:22
Though now I see that JM in the comments has beat me to it... – bill s Apr 18 '17 at 01:48
@bill, I upvoted, don't fret. ;) I didn't answer because I was expecting you'd fix yours. – J. M.'s missing motivation Apr 18 '17 at 01:48
J.M.: You deserve the "win." Post and I'll accept it. Otherwise, I'll go with bill s. Regardless: Thanks you two! – David G. Stork Apr 18 '17 at 01:49

Mr.Wizard · Answer 2 · 2017-04-18T10:40:24.227

If you really want to use "VisibleSpectrum" it can be supplied directly in Blend:

ListLinePlot[
  Table[{x, Sin[x/400]}, {x, 400, 700, 5}]
  , ColorFunction -> (Blend["VisibleSpectrum", #] &)
  , ColorFunctionScaling -> False
  , Filling -> Axis
]

However I recommend that you do not use that inaccurate function but instead:

ChromaticityPlot;  (* pre-load internals *)

newVisibleSpectrum =
  With[
    {colors =
      {Image`ColorOperationsDump`$wavelengths,
       XYZColor @@@ Image`ColorOperationsDump`tris}\[Transpose]},
    Blend[colors, #] &
  ];

ListLinePlot[
  Table[{x, Sin[x/400]}, {x, 400, 700, 5}]
  , ColorFunction -> newVisibleSpectrum
  , ColorFunctionScaling -> False
  , Filling -> Axis
]

See: A better "VisibleSpectrum" function?

Or with newVSgray also from there:

That provides the closest unclipped representation possible within sRGB.

score 1 · Answer 3 · answered Apr 18 '17 at 07:00

You can also use Interpolation

data = Table[{λ, Sin[λ/400]}, {λ, 400, 700, 5}];

f = Interpolation[data];

Plot[f[λ], {λ, 400, 700}, 
 ColorFunction -> Function[{x, y}, ColorData["VisibleSpectrum"][x]],
 ColorFunctionScaling -> False,
 Filling -> Axis, FillingStyle -> Automatic,
 Axes -> False,
 Frame -> {{True, False}, {True, False}},
 FrameLabel -> (Style[#, 14, Bold] & /@
    {"Wavelength (nm)", "Intensity"})]

Filling a ListPlot with an optical spectrum

3 Answers3