4

I have two equations like these. I want to create a for loop that gives to me all intersection points of the two equations. How can I do that? 

 Plot[{x*BesselJ[1, x]*BesselK[0, Sqrt[
     22.295^2 - x^2]]/(BesselJ[0, x]*
      BesselK[1, Sqrt[22.295^2 - x^2]]), Sqrt[22.295^2 - x^2]}, {x, 0,
   23}]

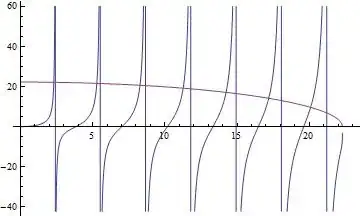
Graph for my equations

halil ibrahim Binici
  • 51
  • 2

1 Answers1

0

try this

NSolve[{x*BesselJ[1, x]*
  BesselK[0, 
    Sqrt[22.295^2 - x^2]]/(BesselJ[0, x]*
     BesselK[1, Sqrt[22.295^2 - x^2]]) - Sqrt[22.295^2 - x^2]} == 
0 && 0 < x < 23, x]

{{x -> 2.30141}, {x -> 5.28092}, {x -> 8.27351}, {x -> 14.2381}, {x -> 17.1905}, {x -> 20.0892}}

EDIT

there is one more root x->11,2619

(see comments below)

ZaMoC
  • 6,697
  • 11
  • 31
  • This does not return all roots that the OP's plot is showing. – Szabolcs Apr 18 '17 at 10:11
  • @Szabolcs The "extra roots" are the asymtotes of this function – ZaMoC Apr 18 '17 at 10:12
  • I meant the root near 11.2619479668904. – Szabolcs Apr 18 '17 at 10:17
  • Reduce does seem to work. It gives a warning that it couldn't prove that all roots were returned, but none seem to be missing: Reduce[x*BesselJ[1, x]* BesselK[0, Sqrt[22.295^2 - x^2]]/(BesselJ[0, x]* BesselK[1, Sqrt[22.295^2 - x^2]]) - Sqrt[22.295^2 - x^2] == 0 && 0 < x < 23, x] – Szabolcs Apr 18 '17 at 10:19
  • I just saw that! why do you think mathematica skipped that one? – ZaMoC Apr 18 '17 at 10:24
  • Well, numerical algorithms tend not to be perfect this way. I don't know how NSolve handles this sort of equation. If I were to use FindRoot, I might just try several starting points for Newton's method, maybe taken from a regular grid. It is clear that that might easily miss roots. findAllRoots (from the first comment) is a bit smarter, and uses Plot to detect zero-crossings, then refines those with FindRoot. But then it gets all those "fake roots". The end result should be filtered. – Szabolcs Apr 18 '17 at 10:31
  • The amazing thing about Reduce is that in some cases it actually guarantees that the result has all* solutions. I do not understand how it does that, or how it can be done in general, but you can read a bit here: http://blog.wolfram.com/2008/12/18/mathematica-7-johannes-kepler-and-transcendental-roots/ This is a pretty unique ability of Mathematica, as far as I know. – Szabolcs Apr 18 '17 at 10:33