3

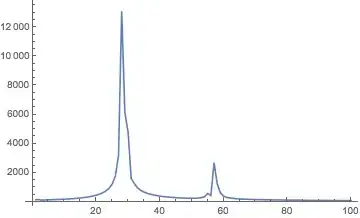
How i can find a frequency from graph after i solve equation by using NDsolve. I try to find frequency, and after that i want to plot a graph frequency versus alpha. This is my code

g = 1
w = 3                      (*frequency*)
y = 1                       (*nonlinearity*)
V0 = 5.74             (* external potential*)
q0 = 0.1              (*alpha*)
A0 = 1                    (* initial amplitude*)
d0 = -0.5             (* initial center-of-mass position*)
a0 = 1                    (* initial width*)
I1 = 2*V0*q0*a[t]*Sqrt[π]*d[t]           
I2 = 2*V0*q0*a[t]^3*d[t]*Sqrt[π]/2        
I3 = 2*V0*q0*a[t]^3*Sqrt[π]/2                     
Q1 = V0*a[t]^3*Sqrt[π]/2 + V0*a[t]*d[t]^2*Sqrt[π]                                    
Q2 = V0*a[t]^5*(3 Sqrt[π])/4 + V0*a[t]^3*d[t]^2*Sqrt[π]/2                             
F = Sqrt[π]/2*V0*A[t]^2*a[t]^3 + Sqrt[π]*V0*A[t]^2*a[t]*d[t]^2


s = NDSolve[{
A'[t] ==  A[t]*b[t] - (I2*A[t])/(Sqrt[π]*a[t]^3) + (3*A[t]*I1)/( 2*Sqrt[π]*a[t]),                  

k'[t] == (2*Sqrt[π]*V0*A[t]^2*a[t]*d[t])/(  Sqrt[π]*A[t]^2*a[t]) + (4*b[t]*I3)/( Sqrt[π]*a[t]),             

a'[t] == -2*a[t]*b[t] - I1/Sqrt[π] + (2*I2)/( Sqrt[π]*a[t]^2),               

d'[t] == -k[t] + (2*I3)/(Sqrt[π]*a[t]),           

b'[t] == -(1/(2*a[t]^4)) + 2*b[t]^2 + (y*A[t]^2)/( 2*Sqrt[2]*a[t]^2) + (g*A[t]^2*a[t])/( 2*Sqrt[2]*(a[t]^2 + w^2)^(3/2)) + (2*Q2)/(Sqrt[π]*a[t]^5) -      Q1/(Sqrt[π]*a[t]^3),                    

A[0] == 1, k[0] == 0.1, a[0] == 1, d[0] == -0.5, b[0] == 0}, {A, k,
a, d, b}, {t, 0, 50}]


  ysol[t_] := d[t] /. s[[1]]

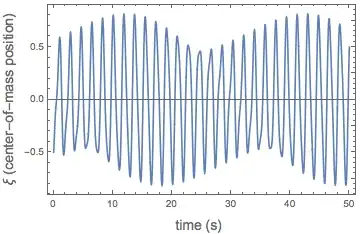
 (*plot graph for center-of-mass position versus time*)
 Plot[ysol[t], {t, 0, 50}, Frame -> True, PlotRange -> {All, All}, 
 FrameLabel -> {StyleForm["time (s) ", FontSize -> 14], 
  StyleForm["ξ (center-of-mass position)", FontSize -> 14]}]

How i can find frequency from peak to peak? what code i should use.

Kuba
  • 136,707
  • 13
  • 279
  • 740
Hyouka Sayrinn
  • 33
  • 3
  • 1
    Related/duplicate: https://mathematica.stackexchange.com/questions/127167/how-to-find-period-of-the-interpolating-function/127172#127172 – Michael E2 Apr 19 '17 at 02:21

1 Answers1

4

You can find the frequencies using the FFT. Starting from your solution for ysol

enter image description here

ydis = Table[ysol[i], {i, 0, 50, 0.001}];
fft = Fourier[ydis, FourierParameters -> {1, -1}];
ListLinePlot[shortFFT = Abs[fft[[1 ;; 100]]], PlotRange -> All]
FindPeaks[shortFFT]

enter image description here

{{2, 164.085}, {28, 13097.5}, {57, 2696.74}}

The two major peaks represent the two major frequencies, which occur at FFT indices 28 and 57. Since the signal ysol was sampled at 1000 Hz (time intervals of 0.001 sec), these represent frequencies of 0.28 and 0.57 Hz. Perhaps this represents a periodic wave with two major harmonics.

Alternatively, one could directly look for the positions of the peaks in ysol.

ydis = Table[ysol[i], {i, 0, 50, 0.001}];
indPeaks = Differences[First@Transpose[FindPeaks[ydis]]];
dist = Mean[indPeaks] // N
1000/dist

1813.56
0.551403

Using this method, there are an average of 1813 samples between peaks, which is about 1.8 sec between peaks, for a frequency of about 0.55 Hz.

bill s
  • 68,936
  • 4
  • 101
  • 191
  • i want to ask for x and y axis, what it represent, respectively? and how to find the coordinate {28, 13097.5}, what code that i must use to show that coordinate? – Hyouka Sayrinn Apr 20 '17 at 05:25
  • The code is just above the output in each case. Thus FindPeaks[shortFFT] gives the {28, 13097.5}. – bill s Apr 20 '17 at 13:28