What is the idiomatic way to operate on the components of an image separately?

Question

Suppose I have an image containing several morphological components and I wish to extract them as individual images (with sizes equal to their bounding boxes; these individual images shouldn't contain parts of neighboring components), then apply some image-processing functions to each of them individually, and finally combine them backward keeping the position of the each as it was in the original image. Note that bounding boxes of the components can intersect with each other.

Here is an example:

img = Import["https://i.stack.imgur.com/QwfYD.png"]

m = MorphologicalComponents[img];
cm = ComponentMeasurements[{m, ColorNegate@img}, {"MaskedImage", "BoundingBox"}];
newComps = ImageAdjust /@ DistanceTransform /@ ColorNegate /@ cm[[;; , 2, 1]]

The question:
How to assemble the transformed components newComps into the complete image?

1

Is this answer of any help? – C. E. Apr 24 '17 at 18:40

Alexey Popkov · Answer 1 · 2017-05-07T13:12:51.487

Here is a SparceArray version of Ali's second method which is expected to be more memory-efficient (at least for images of type "Real"):

{iW, iH} = ImageDimensions@img; 

Image[Total[
  Table[SparseArray[
    Band[1 + Round@{iH - #[[2, 2]], #[[1, 1]]} &@cm[[i, 2, 2]]] -> 
     ImageData[newComps[[i]]], {iH, iW}], {i, Length[cm]}]]]

Procedural summation is even more memory-efficient:

Module[{sum = 0}, 
 Do[sum += SparseArray[
    Band[1 + Round@{iH - cm[[i, 2, 2, 2, 2]], cm[[i, 2, 2, 1, 1]]}] -> 
     ImageData[newComps[[i]]], {iH, iW}], {i, Length[cm]}]; Image[sum]]

Image[Fold[Plus[#1, 
    SparseArray[
     Band[Round@{-cm[[#2, 2, 2, 2, 2]], 1 + cm[[#2, 2, 2, 1, 1]]}] -> 
      ImageData[newComps[[#2]], Automatic], {iH, iW}]] &, 0, Range[Length@cm]]]

Here is how this method can be applied to a three-channel RGB image (the purpose here is to ImageAdjust the components of the image independently from each other):

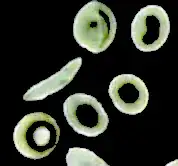
img = Import["https://i.stack.imgur.com/U7zdU.png"]

m = MorphologicalComponents[img, .3];
cm = ComponentMeasurements[{m, img}, {"MaskedImage", "BoundingBox"}];
newComps = ImageAdjust@ImageMultiply[RemoveAlphaChannel@#, AlphaChannel[#]] & /@ 
  cm[[;; , 2, 1]]

{iW, iH} = ImageDimensions@img;

Image[Total[
  Table[SparseArray[
    Band[Round@{1 + iH - #[[2, 2]], 1 + #[[1, 1]], 1} &@cm[[i, 2, 2]]] -> 
     ImageData[newComps[[i]]], {iH, iW, 3}], {i, Length[cm]}]]]

Combining everything into one function:

assembleComponents[newComps_, boundingBoxes_, {iW_, iH_}] := 
 Module[{sum = 0, iCh = ImageChannels[newComps[[1]]]},
  If[iCh == 1, 
   Do[sum += SparseArray[
      Band[Round@{iH - boundingBoxes[[i, 2, 2]] + 1, boundingBoxes[[i, 1, 1]] + 1}] -> 
       ImageData[newComps[[i]], Automatic], {iH, iW}], {i, Length[boundingBoxes]}],
   Do[sum += 
     SparseArray[
      Band[Round@{iH - boundingBoxes[[i, 2, 2]] + 1, boundingBoxes[[i, 1, 1]] + 1, 1}] -> 
       ImageData[newComps[[i]], Automatic], {iH, iW, iCh}], {i, Length[boundingBoxes]}]]; 
  Image[sum]]

Usage:

assembleComponents[newComps, cm[[;; , 2, 2]], ImageDimensions[img]]

Fun,since we want to restore the image,then we have no the information of img.Then we cannot use ImageDimensions@img? — yode, Apr 25 '17 at 21:29
@yode No, you misunderstood the question. We don't need to restore the original image, we have it. We need to assemble processed components into the complete new image in a way that each of them is placed exactly where it was in the original image. — Alexey Popkov, Apr 25 '17 at 22:16

Ali Hashmi · Answer 2 · 2017-04-24T20:08:59.880

5

Module[{seg, img = img, cm, newComps, func},

seg = MorphologicalComponents[img];
cm = ComponentMeasurements[{seg, ColorNegate@img}, {"MaskedImage","BoundingBox"}];
newComps = ImageAdjust /@ DistanceTransform /@ ColorNegate /@ cm[[;; , 2, 1]];

func[matrix_, {ind_, imgs_}] := 
Block[{mat = matrix, cellindpos, smallImgData, vals},
cellindpos = Position[seg, ind];
smallImgData = ImageData@imgs;
vals = Extract[#, Position[#, x_ /; x != 0]] &@smallImgData ;
ReplacePart[mat, Thread[cellindpos -> vals]]
];

Fold[func, ConstantArray[0, Reverse@ImageDimensions@img],
Thread[{Range@Length@newComps, newComps}]]] // Image

edited Apr 24 '17 at 20:08

answered Apr 24 '17 at 19:09

Ali Hashmi

8,950
4
22
42

This method assumes that the indices of each of the components do not change during processing of the subimages. This assumption is very restrictive and isn't correct in general. Your second method is much better since it doesn't imply such an assumption and at the same time is much simpler and more efficient. – Alexey Popkov Apr 25 '17 at 16:51

score 4 · Answer 3 · edited Apr 28 '17 at 18:54

4

An ArrayPad version of Ali's second method:

data = KeyValueMap[
  Round[Transpose[#2]] -> ImageData[#1] &, <|Thread[newComps -> cm[[All, -1, -1]]]|>];
dim = ImageDimensions[img];
Image[Plus @@ (ArrayPad[Values[#], {{dim[[2]] - Keys[#1][[2, 2]], 
   Keys[#1][[2, 1]]-1}, {Keys[#1][[1, 1]]-1,dim[[1]] - Keys[#1][[1, 2]]}}] & /@ data)]

Mathematica graphics

edited Apr 28 '17 at 18:54

Alexey Popkov

61,809
7
149
368

answered Apr 25 '17 at 02:22

yode

26,686
4
62
167

Since we have img, you should simply use dim = ImageDimensions[img] for obtaining the dimensions of the original image. Then your solution won't be "durty" anymore. ;) – Alexey Popkov Apr 28 '17 at 12:54
@AlexeyPopkov Pretty a little,thanks. – yode Apr 28 '17 at 13:08
I've added a short description of your method, I hope you don't mind. :) – Alexey Popkov Apr 28 '17 at 18:55
@AlexeyPopkov Not at all,be my guest.But actually I havenot see the Ali's answer.If I have,I would not post it. :) – yode Apr 28 '17 at 21:11

Ali Hashmi · Answer 4 · 2017-04-24T20:09:47.367

3

{comps, boxes} = Module[{seg, img = img, cm, newComps, bounds},
seg = MorphologicalComponents[img];
cm = ComponentMeasurements[{seg, ColorNegate@img}, {"MaskedImage","BoundingBox"}];
bounds = cm[[All, 2, 2]];
newComps = ImageAdjust /@ DistanceTransform /@ ColorNegate /@ cm[[;; , 2, 1]];
{newComps, bounds}];

{iW, iH} = ImageDimensions@img

ImageAdd[MapThread[ImagePad[#1, {{#2[[1, 1]], iW - #2[[2, 1]]}, {#2[[1, 2]], 
  iH - #2[[2, 2]]}}] &, {comps, boxes}]]

edited Apr 24 '17 at 20:09

answered Apr 24 '17 at 20:04

Ali Hashmi

8,950
4
22
42

This method uses ImagePad and since the approach is different hence posting it as a separate answer. Also the image obtained from this and the previous answer are both same (tested using SameQ) – Ali Hashmi Apr 24 '17 at 20:05
@AlexeyPopkov please feel free to modify the answer. will be happy to see the modification ! – Ali Hashmi Apr 24 '17 at 20:19
@AlexeyPopkov at the end of both methods we can replace all background pixel values to the desired colour – Ali Hashmi Apr 24 '17 at 20:25

Alexey Popkov · Answer 5 · 2017-05-03T13:31:18.793

If instead of "BoundingBox" we request "Mask" the solution becomes more elegant and idiomatic:

cm = ComponentMeasurements[{m, ColorNegate@img}, {"MaskedImage", "Mask"}, 
   "PropertyAssociation"];

newComps = ImageAdjust /@ DistanceTransform /@ ColorNegate /@ cm["MaskedImage"];

pos = Min /@ Transpose[#["NonzeroPositions"]] & /@ cm["Mask"];

Image[Total[
  Table[SparseArray[Band[pos[[i]]] -> ImageData[newComps[[i]]], 
    Reverse[ImageDimensions@img]], {i, Length[newComps]}]]]

What is the idiomatic way to operate on the components of an image separately?

5 Answers5

Linked