Neumann boundary condition for Laplace equation

Question

I have a solution for the Laplace equation with simple Dirichlet boundary conditions. The top side of the square is kept constant at 100 while other sides are fixed at 0. The code is here:

ClearAll["Global`*"]
Needs["NDSolve`FEM`"]

square = Rectangle[{0, 0}, {10, 10}];
mesh = ToElementMesh[DiscretizeRegion[square], MaxCellMeasure -> 0.01];

bc = {
   DirichletCondition[u[x, y] == 0, y == 0 || x == 10 || x == 0],

   DirichletCondition[u[x, y] == 100, y == 10]
   };

sol = NDSolveValue[{D[u[x, y], x, x] + D[u[x, y], y, y] == 0 , bc}, 
   u, {x, y} \[Element] mesh];

DensityPlot[sol[x, y], {x, y} \[Element] mesh, Mesh -> None, 
 ColorFunction -> "Rainbow", PlotRange -> All, 
 PlotLegends -> Automatic]

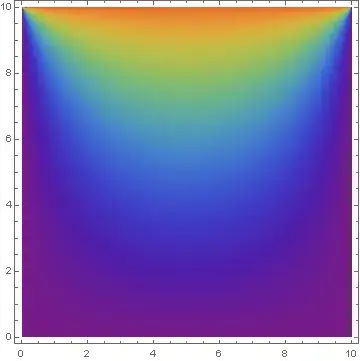
Here is the plotted solution:

Now what I would like to do is to set Neumann boudary conditions for the left and right walls. I want to fix the gradient at 0 for these two walls.

I approach it by getting rid of || x == 10 || x == 0 in the old boundary condition setup and introducing:

Derivative[1,0][u][0,y] == 0,
Derivative[1,0][u][10,y] == 0

This doesn't work for me. Could you please help me find the mistake?

Answer 1

One approach is to leave out the homogeneous Neumann boundary conditions when using FEM as mentioned by @andre in the comment.

The other is to include it,

nv1 = NeumannValue[0, x == 0];
nv2 = NeumannValue[0, x == 10];
bc = {DirichletCondition[u[x, y]== 0, y == 0],DirichletCondition[u[x, y] == 100, y == 10]};

sol = NDSolve[{D[u[x, y], x, x] + D[u[x, y], y, y] == nv1 + nv2, bc}, 
   u, {x, y} ∈ mesh, Method -> {"FiniteElement"}];

DensityPlot[u[x, y] /. sol, {x, y} ∈ square, ColorFunction -> "Rainbow", 
      PlotRange -> All, PlotLegends -> Automatic]

Having no affect on the results whether you include it or not when using FEM.