Count works differently depending on how an association was created

Question

Bug introduced in 10.4 and fixed in 11.3.0

---

I create two associations, that are supposed to be exactly the same. And then I want to count the elements at the second level. And I get different results:

x = Range[2];
a1 = <|"a" -> x|>;
a2 = <|"a" -> {1, 2}|>;
a1
a2
a1 === a2
Count[a1, _, {2}]
Count[a2, _, {2}]

<|"a" -> {1, 2}|>

<|"a" -> {1, 2}|>

True

0

2

It just doesn't make sense to me. What is going on?

Answer 1

As Kirill Belov notes in a comment, the issue is related to the fact that the list a1 is a packed array (generated by Range) whereas the list a2 is not packed. Count, Position and Depth unexpectedly act as if the packed array is atomic. This is very likely a bug since 1) the expected behaviour occurs if the top-level expression is a list instead of an association and 2) many other level-sensitive functions yield the expected results.

Analysis (current as of version 11.1)

For discussion purposes, let us consider the following two associations:

packed =   <| "a" -> Developer`ToPackedArray[{1, 2}] |>;
unpacked = <| "a" -> Developer`FromPackedArray[{1, 2}] |>;

We will apply various operators to these values:

The results show that Count, Position and Depth act as if the packed array were atomic. The results for these operations can be explained by the TreeForm structure diagrams shown in the table if we consider all of the internal association structural details to be a "single level" (i.e. the AssociationNodes from Assocation down to Rule).

On the other hand, these results are not consistent with those operations that appear in the table below the structure diagrams. Cases, Level, Total, Map and Replace all treat the packed array as if it were not atomic.

Furthermore, even Count, Position and Depth stop treating the packed array as atomic if the top-level expression is a list instead of an association:

We can see from this second table the results are all consistent for the various level-sensitive operators -- except when Count, Position and Depth acting upon a packed array contained within an association. This is almost certainly a bug.

Answer 2

I don't know why, but this works:

x = Range[2]; 
a1 = ToExpression[ Association["a" -> x]]; 
a2 = Association["a" -> {1, 2}]; 
a1
a2
a1 === a2
Count[a1, _, {2}]
Count[a2, _, {2}]

Answer 3

It really depends on how to define an evaluation. For instance, the Association is <|"a" -> "PackedArray"[Integer, "<" 2 ">"]|>, Some people think it's evaluated and this is the irreducible value, I think it's not evaluated or a special form. No matter you know it's a PackedArray or not, if you treat x as an unevaluated symbol, it would be not a surprise to see such a result. Nevertheless, It's good to know it's a PackedArray.

There are some examples which can prove x3 = Range[2] is not "evaluated"/ in a special form.

This issue is a bit tricky, it's related to Range function, if you use x3 = Table[i, {i, 2}], you will not have this issue.

CountAssociation[x_, level_] := 
 Count[Association["a" -> x], _, {level}]

x1 = {{1, 2}, {1, 2}, {1, 2}}
x3 = Range[2]

CountAssociation[x1, 2] (*3*)
CountAssociation[x1, 3] (*6*)

CountAssociation[{x3}, 2] (*1*)
CountAssociation[{x3, 
  x3}, 2] (*2*)
CountAssociation[{x3, x3, 
  x3}, 2](*3*)
CountAssociation[x3, 2](*0*)
CountAssociation[{x3}, 3](*0*)

In:

Remove[a1, x1, x2] 
x1 = Range[2];
x2 = {1, 2};
CountAssociation[x_] := Count[Association["a" -> x], _, {2}]
CountAssociation[x1]
CountAssociation[x2]

Out:

0
2

Both of x1 and x2 are not stateful computation, Use x1 and x2 as inputs to CountAssociation respectively, the outputs are different.

CountAssociation has not side effect, in other words, CountAssociation's input decides the output, the same inputs always output the same result. (Assuming the Inputs are not stateful computation)

It means x1 and x2 are not the same input.

Why? It's about lazy evaluation and force evaluation. Please check the code below.

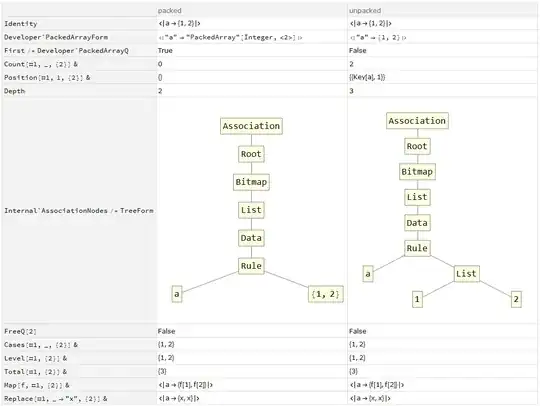
When you print x in Mathematica, x is evaluated, so you can see the evaluated result of x. However x isn't evaluated when you use x to construct an association or assign x as a value of an association.

x is not evaluated, x is symbol but not a list to Count, that's why the result is 0 but not 2.

To solve this issue you have to force evaluate x to a list, you can use Map[Identity].

In:

Remove[a1, y]
y
a1 = <|"a" -> y|>;
Count[a1, _, {2}]

Remove[a1, x]
x = Range[2] // Map[Identity]
a1 = <|"a" -> x|>;
Count[a1, _, {2}]

Remove[x, a1]
x = Range[2];
a1 = <||>;
a1["a"] = x // Map[Identity]
Count[a1, _, {2}]

Out:

y
0

{1, 2}
2

{1, 2}
2