How to pad periodically a cube to be compatible with ListInterpolation?

Question

Context

I would like to define a periodic interpolation function on a cube. It seems mathematica's ListInterpolation and the option PeriodicInterpolation -> True cannot cope with a cube which is not explicitly periodic. So I need to pad periodically this cube so as to interpolate it.

Question

How to pad a given cube so that ListInterpolation over this padded cube accounts for periodicity?

Attempt

Let me start with a trivial cube

dat = Range[2^3] // Partition[#, {2}] & // Partition[#, {2}] &

Following This link MrWizard's nifty command periodically pads the cube

 dat = PadRight[dat, Dimensions[dat] + 1];
 a = {0, 1}~Tuples~TensorRank[dat]~SortBy~Tr // Rest;
 MapThread[(dat[[Sequence @@ #]] = dat[[Sequence @@ #2]]) &, {-a, 
    a} /. 0 -> All];

Now dat has the right structure for ListInterpolation

{{{1, 2, 1}, {3, 4, 3}, {1, 2, 1}}, {{5, 6, 5}, {7, 8, 7}, {5, 6, 5}}, {{1, 2, 1}, {3, 4, 3}, {1, 2, 1}}}

And indeed Mathematica's ListInterpolation takes the periodic table

f = ListInterpolation[dat,PeriodicInterpolation -> True, InterpolationOrder -> 0]

 dat[[2, 1, ;; -2]]

{10,11,12}

 Table[f[2, 1, x], {x, 1, 3}]

{10,11,12}

and the interpolation is indeed periodic

Table[f[2, 1, x], {x, 1, 6}]

{10,11,12,10,11,12}

But if I apply the same technique to a random table

dat =RandomVariate[NormalDistribution[], 3^3]//Partition[#, {3}] & //Partition[#, {3}] &
dat =PadRight[dat, Dimensions[dat] + 1];a ={0, 1}~Tuples~TensorRank[dat]~SortBy~Tr // Rest;
MapThread[(dat[[Sequence @@ #]]=dat[[Sequence @@ #2]]) &,{-a,a}/.0 -> All];
f = ListInterpolation[dat,PeriodicInterpolation -> True,InterpolationOrder-> 0]

Even though the cube has been made periodic:

dat[[2, 1, ;;]]

{0.87581,-0.125233,-0.497163,0.87581}

The interpolation produces nonsense

 Table[f[2, 1, x], {x, 1, 3}]

{-0.305603,-0.305603,-1.6259}

My guess is that I am missing something obvious, but the answer might be of interest to this community nonetheless? I wish the builtin function would deal transparently with this !

Update

When considering it more globally,the solution does not seem to be fully satisfactory.

If I generate a 16x16 Gaussian random field using this function.

 dat = GaussianRandomField[nn = 16, 2, Function[k,k^(-1.5)]]//Chop//GaussianFilter[#, 4] &;

Then

dat = PadRight[dat, Dimensions[dat] + 1];a = {0,1}~Tuples~TensorRank[dat]~SortBy~Tr//Rest;
MapThread[(dat[[Sequence @@ #]] = dat[[Sequence @@ #2]]) &, {-a, 
    a} /. 0 -> All]; dat[[;; , ;;]] // MatrixPlot

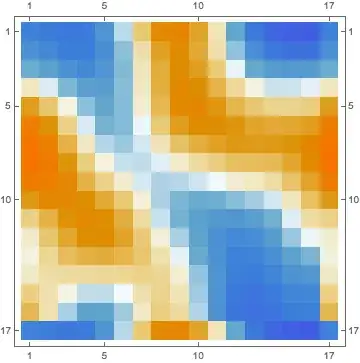
Then the ListInterpolation does not seem to be truly periodic.

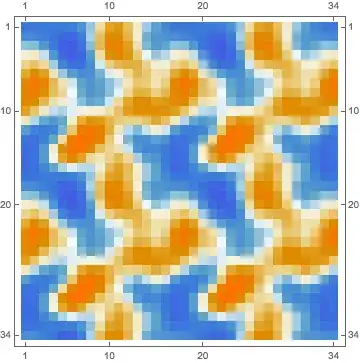
f = ListInterpolation[dat, PeriodicInterpolation -> True];
Map[ f @@ # &, Outer[List, Range[32], Range[32]], {2}] // MatrixPlot

Answer 1

Some of the problem seems to arise from the Gaussian Filtering which is not periodic. If periodic Filtering is done in Fourrier Space (via the Exp[-( k/2)^2] cutoff), then it seems to work:

dat = GaussianRandomField[nn=16,3,Function[k, Exp[-(k/2)^2]k^(-1.5)]] //Chop; 
dat = PadRight[dat, Dimensions[dat] + 1];
a = {0, 1}~Tuples~TensorRank[dat]~SortBy~Tr // Rest;
MapThread[(dat[[Sequence @@ #]] = dat[[Sequence @@ #2]]) &, {-a,a} /. 0 -> All]; 
dat[[;; , ;; , 1]] // MatrixPlot

Then the interpolation seems to work:

f = ListInterpolation[dat, PeriodicInterpolation -> True,
   InterpolationOrder -> 3]; Map[ f @@ # &,  
  Outer[List[#1, #2, 1] &, Range[Length[dat]*2], 
   Range[Length[dat]*2]], {2}] // MatrixPlot

Also true when slicing in the other direction:

Map[ f @@ # &,  Outer[List[#1, 1, #2] &, Range[Length[dat]*2], 
   Range[Length[dat]*2]], {2}] // MatrixPlot

It can be encapsulated as follows

Clear[ListInterpolationPeriodic]; 
ListInterpolationPeriodic[dat_List, opts___] := Module[{a, dat1},
  dat1 = PadRight[dat, Dimensions[dat] + 1];
  a = {0, 1}~Tuples~TensorRank[dat]~SortBy~Tr//Rest;
  MapThread[(dat1[[Sequence @@ #]]=dat1[[Sequence @@ #2]]) &,{-a,a}/. 0-> All];
  ListInterpolation[dat1, PeriodicInterpolation -> True,opts]]

f = ListInterpolationPeriodic[dat, InterpolationOrder -> 2]

All the credits goes to MrWizard.