Combine two matrices of unequal dimensions

Question

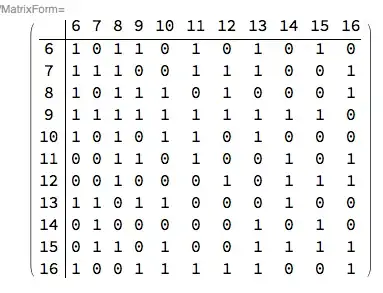
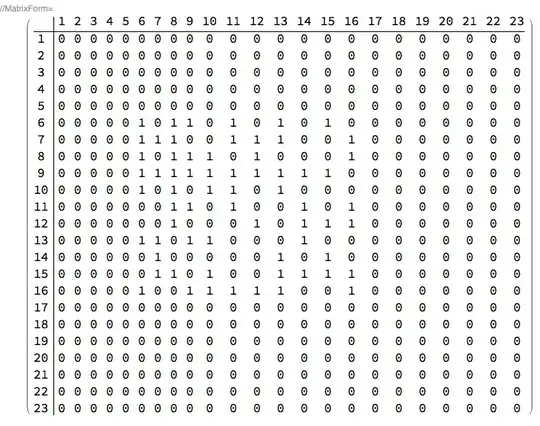
I have a 11x11 matrix and a 23x23 one. The 23x23 is a null matrix and I need to insert the 11x11 matrix in the null matrix for a specific position of the element 6,6 in the first matrix like this:

aaaaaaaaaaa000000000000

00000000000000000000000

So element 6,6 at the first matrix is inserted at the position 6,6 at the second matrix. The elements of the first matrix are not all the same, it is a generic set of data. I need to be able to put the element 6,6 in any position of the second matrix, assuming that it won't overflow the limit of 23x23. How can I do that?

Jack LaVigne · Answer 1 · 2019-11-22T19:55:08.473

8

Assuming that you want to insert the 11x11 into the 23x23 at position {6,6}

n = ConstantArray[0, {23, 23}];
m = RandomInteger[1, {11, 11}];

First make a copy of n if you want to keep it (you could work directly with n if it was not needed).

newMatrix = n;

Next equate specific elements of newMatrix with m.

newMatrix[[6 ;; 16, 6 ;; 16]] = m;

Here is what it looks like

newMatrix // MatrixForm

Mathematica graphics

edited Nov 22 '19 at 19:55

answered May 14 '17 at 00:11

Jack LaVigne

14,462
2
25
37

score 7 · Answer 2 · answered May 14 '17 at 00:36

Since the matrix into which you wish to insert is all zeros you can simply PadRight the input matrix. I'll use dimensions 5x5 and 11x11 to keep the examples manageable.

SeedRandom[0]

input = RandomInteger[9, {5, 5}]

$\left( \begin{array}{ccccc} 7 & 0 & 8 & 2 & 1 \\ 5 & 8 & 0 & 6 & 7 \\ 2 & 1 & 0 & 6 & 1 \\ 2 & 8 & 6 & 5 & 5 \\ 8 & 4 & 5 & 9 & 0 \\ \end{array} \right)$

This embeds into an 11x11 array starting three rows down and one column in:

PadRight[input, {11, 11}, 0, {3, 1}]

$\left( \begin{array}{ccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 7 & 0 & 8 & 2 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 5 & 8 & 0 & 6 & 7 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 1 & 0 & 6 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 8 & 6 & 5 & 5 & 0 & 0 & 0 & 0 & 0 \\ 0 & 8 & 4 & 5 & 9 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \right)$

You can also use ArrayPad but you'll need to calculate the dimensions:

ArrayPad[input, {{3, 3}, {1, 5}}]

(* same output *)

score 4 · Accepted Answer · answered May 13 '17 at 23:09

4

Here is one way:

n=ConstantArray[0,{23,23}];
m=RandomInteger[1,{11,11}];

With[{i=10,j=10},
  ReplacePart[n,Select[
      Flatten@MapIndexed[(#2-{6-1,6-1}+{i-1,j-1})->#1&,m,{2}],
      AllTrue[First@#,Between[#,{1,23}]&]&
    ]
  ]
]//MatrixForm

It puts the element $6,6$ in position $i=10,j=10$.

answered May 13 '17 at 23:09

swish

7,881
26
48

Thanks, Kenny. I ended up doing like this: newM = Sum[ Sum[SparseArray[{Band[{(3j + 1), (3i + 1)}] -> M}, {n, n}], {i, 0, (d - 1)}], {j, 0, (d - 1)}];, so I can also sum all the combinations I need at the same time :p – Rodrigo May 13 '17 at 23:33

score 3 · Answer 4 · answered May 14 '17 at 02:27

The reason to post this answer is that although it is longer than a dedicated answer, its code shows the systematic use of the package RSparseMatrix for these kind of tasks.

Import["https://raw.githubusercontent.com/antononcube/\
MathematicaForPrediction/master/Misc/RSparseMatrix.m"]

mat0 = ConstantArray[0, {23, 23}];
mat1 = RandomInteger[1, {11, 11}];

rmat0 = ToRSparseMatrix[SparseArray[mat0], 
   "RowNames" -> Map[ToString, Range[Dimensions[mat0][[1]]]], 
   "ColumnNames" -> Map[ToString, Range[Dimensions[mat0][[2]]]]];

rmat1 = ToRSparseMatrix[SparseArray[mat1], 
   "RowNames" -> Map[ToString, Range[Dimensions[mat1][[1]]]], 
   "ColumnNames" -> Map[ToString, Range[Dimensions[mat1][[2]]]]];

SetRowNames[rmat1, 
  Map[ToString, (6 - 1) + Range[Dimensions[mat1][[1]]]]];
SetColumnNames[rmat1, 
  Map[ToString, (6 - 1) + Range[Dimensions[mat1][[2]]]]];

rmat1 // MatrixForm

rmat2 = ImposeColumnNames[
          ImposeRowNames[rmat1, RowNames[rmat0]], 
          ColumnNames[rmat0]];
rmat2 // MatrixForm

Also see these answers:

Combine two matrices of unequal dimensions

4 Answers4