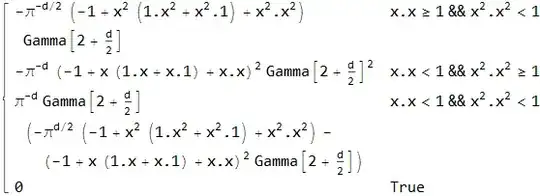Inspired by this question I try to find to compute the variance of: $$f(\vec{t}) = \cases{\frac{d + 2}{2 c_d}(1 - \vec{t} \cdot \vec{t}) & if $\vec{t} \cdot \vec{t}< 1$ \\0 & otherwise}$$
where $c_d$ is the volume of the unit sphere of dimension $d$:
$$ c_d = \frac{\pi^{d/2}}{\Gamma\left(\frac{d}{2} + 1\right)},$$ according to: $$E[x] = \int_{-\infty}^{\infty} x \cdot f(x) \; dx$$ and $$VAR[x]= E[x^2] - \left(E[x]\right)^2.$$
I tried to do this with the following mathematica code
$Assumptions = {d >= 1, Element[d, Integers], Element[x, Vectors[d]]};
unitSphereVolume = pi^(d/2)/Gamma[d/2 + 1];
epan [t_] = Piecewise[{{(d + 2)/(2 * unitSphereVolume) (1 - Dot[t, t]), Dot[t, t] < 1}}, 0];
EV[_t] = Refine[D[t * epan[t], t], Element[t, Vectors[d]]];
V[_t] = Refine[EV[t^2] - (EV[t])^2, Element[t, Vectors[d]]];
FunctionExpand[V[x]]
I want to compute the variance of $f(x)$ as a function of $d$, but evaluating this notebooks gives V[x] as output. What am I missing?