1

To study the change in Laplacian eigenvalues on a spherical segment, I constructed a table of spherical segments using the code from here.

I discretized the output using DiscretizeGraphics and obtained a table of discretized spherical segments.enter image description here.

As I try to apply NDEigensystems on the discretized figures, I get the following error:

enter image description here enter image description here

The code I am using to generate the spherical segments :

sphericalSegment[{r1_,r2_}, {\[Theta]1_, \[Theta]2_}, {\[Phi]1_, \[Phi]2_}]:=
Module[{plot, pts, surf, bdy},plot = ParametricPlot3D[{Cos[\[Theta]] Sin[\[Phi]],Sin[\[Theta]] Sin[\[Phi]],Cos[\[Phi]]}, {\[Theta], \[Theta]1, \[Theta]2}, {\[Phi], \\[Phi]1, \[Phi]2}, Mesh -> None, BoundaryStyle -> Black];
pts = First@Cases[plot, GraphicsComplex[p_, ___] :> p, Infinity];
surf = First@Cases[plot, Polygon[p_] :> p, Infinity];
bdy = First@Cases[plot, Line[p_] :> p, Infinity];
GraphicsComplex[Join[r1*pts, r2*pts], {EdgeForm[], Polygon[surf],  Polygon[Reverse /@ surf + Length@pts],Polygon[Join[#, Reverse@# + Length@pts], VertexNormals -> Cross[Subtract @@ pts[[#]], pts[[First@#]]]] & /@   Partition[bdy, 2, 1, 1]}, VertexNormals -> Join[-pts, pts]]]

Code to calculate the Laplacian Eigenvalues :

r = Flatten[Table[{Graphics3D[sphericalSegment[{1, 1}, {0, 2 Pi}, {Pi/n, Pi}]]}, {n, 1.2, 3, 0.2}]];
dr = DiscretizeGraphics /@ r;
eigs = NDEigensystem[{-Laplacian[f[x, y, z], {x, y, z}] + NeumannValue[0,True]}, f[x, y, z], Element[{x, y, z}, #],1] & /@ dr
SPPearce
  • 5,653
  • 2
  • 18
  • 40
Aritra Saha
  • 87
  • 7

1 Answers1

2

The missing text is

NDEigensystem::femnfm: The current version of NDSolve cannot solve equations over boundaries or surfaces. Please specify a region where the embedding dimension is the same as the dimension.

So your shells need some thickness.

user21
  • 39,710
  • 8
  • 110
  • 167
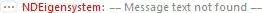
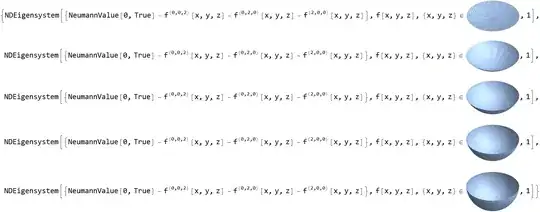
  • off topic question, could EmptyRegion[2] typeset to {} inside Graphics? do you think it is a reasonable request? – Kuba Jun 06 '17 at 08:05
  • @Kuba, Where does this come up? My thinking is that EmptyRegion is not a graphics primitive. You would not expect Graphics[{Line[{{0, 1}, {1, 1}}], DiscretizeRegion[Disk[]]}] to work either. Can you show me an example where this is useful? – user21 Jun 06 '17 at 14:13
  • Everywhere where one wants to quickly show region based computation. e.g. 147287 it would be nice to avoid _EmptyRegion -> Nothing. Or in recent 147708 – Kuba Jun 06 '17 at 14:18
  • The problem I have is probably that RegionInstersection of graphics primitives is not a graphics primitive, in case of EmptyRegion. – Kuba Jun 06 '17 at 14:19
  • 1
    I see, the problem is that making EmptyRegion a graphics primitive would open the argument that every expr should be displayable by Graphics. I'd just use something like ri = RegionIntersection[{Line[{l11, l12}], Line[{l21, l22}]}]; If[Head[ri] === EmptyRegion, {}, ri] But why don't you send a suggestion to support? – user21 Jun 06 '17 at 14:54
  • I wanted to ask you first to check if that makes sense, I'm not using regions on daily basis. – Kuba Jun 06 '17 at 18:51