How to interpolate 3D data

Question

Here comes some sample data

data = {{8.546, 10.3, -3270}, {8.525, 10.2, -3211}, {8.554, 10.1, -3162},
        {8.609, 10, -3120}, {8.709, 9.9, -3085}, {8.966, 9.89, -3084}, 
        {9.204, 9.9, -3083}, {9.421, 10, -3108}, {9.588, 10.1, -3133},
        {9.740, 10.2, -3157}, {9.885, 10.3, -3180}};

L1 = ListPointPlot3D[data, PlotStyle -> {{Darker[Green], PointSize[0.02]}}]

which gives

My question: Is there a way to interpolate these data and obtain much more points between them? I want that many points so as to obtain a smooth solid line in 3D space. Moreover, is it possible to join these data, like the option Joined -> True in ListPlot?

Many thanks in advance!

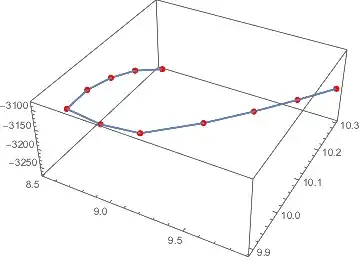
I asked because the unordered case is much harder. In this case, you could just do Show[L1, Graphics3D[{Green, Line[data]}]]. — J. M.'s missing motivation, May 25 '17 at 06:59
@J.M. The line is OK< but what about the interpolation? I need plenty of more data between the points, so as to be able to draw a smooth line. — Vaggelis_Z, May 25 '17 at 07:04
You can modify @J.M.'s method to draw a smooth curve: i.e. Graphics3D[{Green, BSplineCurve[data]}]. It will not go directly through all points, but will produce a nice picture. — Ray Shadow, May 25 '17 at 08:47
@Shadow, you could use a method like the one in this answer to make an interpolating BSplineCurve[], if that is what is wanted. — J. M.'s missing motivation, May 25 '17 at 09:03

Quantum_Oli · Accepted Answer · 2017-05-25T09:45:44.240

Interpolation still works in 3D:

f = Interpolation[Transpose[{Range[Length[data]], data}],   InterpolationOrder -> 1]

Show[
 ListPointPlot3D[data, PlotStyle -> {{Red, PointSize[0.02]}}],
 ParametricPlot3D[f[u], {u, 1, Length[data]}, BoxRatios -> {1, 1, 1}]
]

Sampling

You can choose how you want your sampled points to be spaced. For example you might just want points evenly spaced between your existing points:

tsData1 = With[{u = Rescale@Range[Length[data]]},
  Transpose[{u, data}]
];

f1 = Interpolation[tsData1, InterpolationOrder -> 1]

data1 = Table[f1[u], {u, 0, 1, 0.025}];

ListPointPlot3D[{data1, data}, PlotStyle -> {{Red, PointSize[0.02]}, {Blue, PointSize[0.02]}}]

Or you might want point evenly distributed along the length of the line:

tsData2 = With[{u = 
    Rescale@Prepend[Accumulate[EuclideanDistance @@@ Partition[data, 2, 1]], 0]
  },
  Transpose[{u, data}]
];

f2 = Interpolation[tsData2, InterpolationOrder -> 1]

data2 = Table[f2[u], {u, 0, 1, 0.025}];

ListPointPlot3D[{data2, data}, PlotStyle -> {{Red, PointSize[0.02]}, {Blue, PointSize[0.02]}}]

Can we create a new list data2 containing let's say 1000 interpolated points between the existing ones? — Vaggelis_Z, May 25 '17 at 09:23
Yeah, just data2 = Table[f[u], {u, 1, Length[data], (Length[data] - 1)/(1000 - 1)}] — Quantum_Oli, May 25 '17 at 09:37

score 1 · Answer 2 · answered May 25 '17 at 09:23

So this is the best I could do, maybe improvements can be made, but I don't know. If you want to plot a line, you need to use ParametricPlot3D, which needs inputs along the lines of {x,y(x),z(x)}. So we're going to split your data into two pieces and use interpolation on them. The first datapoint is irritating to the interpolation though, so I left it out.

dataY = Table[{data[[i, 1]], data[[i, 2]]}, {i, 2, Length[data]}];
intY = Interpolation[dataY];
dataZ = Table[{data[[i, 1]], data[[i, 3]]}, {i, 2, Length[data]}];
intZ = Interpolation[dataZ];
Show[{ListPointPlot3D[data,
PlotStyle -> {{Darker[Green], PointSize[0.02]}}, PlotRange -> All],
   ParametricPlot3D[{x, intY[x], intZ[x]}, {x, 8.53, 9.89}]}]

This is the result:

There are probably some improvements that can be made on this, but I think this is the general idea that you should follow.

How to interpolate 3D data

2 Answers2