Getting strange "not a polynomial" error from NDSolve

Question

After answering this question, I decided to change it a bit (had some free time), and turned it into a Gross-Pitaevskii equation. Suddenly, the code that used to work now gives the error message:

CoefficientArrays::poly: "1/2 (-ψ$6110-ψ$6111)+ψ (1-
1/Sqrt[1+x$6089^2+y$6090^2]+0.1 Abs[ψ]^2) is not a polynomial.

I tried changing the potential for the Harmonic Oscillator, but still no use.

My code:

ClearAll["Global`*"];
g = 0.1;
X = 5;
V[x_, y_] := 1/2 (x^2 + y^2);
ini[x_, y_] := Exp[-(x^2 + y^2)];
bc = ψ[x, y] == 
    ini[x, y] /. {{x -> X}, {x -> -X}, {y -> X}, {y -> -X}};
sys = {-1/
       2 (D[ψ[x, y], {x, 2}] + 
        D[ψ[x, y], {y, 2}]) + (V[x, y] + 
        g Abs[ψ[x, y]^2]) ψ[x, y] == Etr ψ[x, y], bc};
sol = ParametricNDSolveValue[
  sys, ψ, {x, -X, X}, {y, -X, X}, {Etr}];
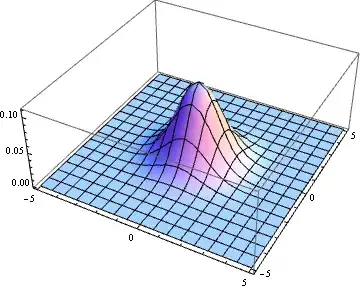
Plot3D[Abs[sol[1][x, y]], {x, -X, X}, {y, -X, X}, PlotRange -> All]

If I set g=0, I get some good results. Any other value and I get the error message.

Can anyone explain what's going on? How can it be fixed?

I think it's simply because "FiniteElement" method can't handle nonlinear equations at the moment… — xzczd, May 26 '17 at 02:02
I tried with g = 0,0.1,0.2,1 etc..and its working fine for me. I am on Mathematica 11.0.0 — Lotus, May 26 '17 at 02:24
@Lotus Have you tried using the sol? I mean, try executing e.g. sol[1]. — xzczd, May 26 '17 at 03:15
Related: https://mathematica.stackexchange.com/questions/87723/fem-giving-is-not-a-polynomial-error — Michael E2, May 26 '17 at 03:28
@xzczd, I tried a few methods and all failed. Is there anyone in particular you feel could work? — ivbc, May 26 '17 at 04:02
I edited the code to have a plot3D command and expose the error more easily. — ivbc, May 26 '17 at 04:06
I see the error messages when I access the function using sol[1]. It is strange. — Lotus, May 26 '17 at 04:11

xzczd · Accepted Answer · 2019-01-30T12:37:32.460

As mentioned in the comments above, currently "FiniteElement" method can't handle nonlinear PDE. Fortunately you're solving the PDE on a regular domain, so let's make a step backward i.e. try solving the equation with finite difference method (FDM). I'll use pdetoae for the generation of difference equations:

g = 0.1;
X = 5;
V[x_, y_] := 1/2 (x^2 + y^2);
ini[x_, y_] := Exp[-(x^2 + y^2)];
bc = ψ[x, y] == ini[x, y] /. {{x -> X}, {x -> -X}, {y -> X}, {y -> -X}};
eq = -1/2 (D[ψ[x, y], {x, 2}] + D[ψ[x, y], {y, 2}]) + (V[x, y] + 
       g Abs[ψ[x, y]^2]) ψ[x, y] == Etr ψ[x, y];

domain = {-X, X};
points = 25;
grid = Array[# &, points, domain];
difforder = 4;

(* Definition of pdetoae isn't included in this post,
   please find it in the link above. *)
ptoafunc = pdetoae[ψ[x, y], {grid, grid}, difforder];

del = #[[2 ;; -2]] &;

ae = del /@ del@ptoafunc[eq];
aebc = MapAt[del, ptoafunc[bc], {{1}, {2}}];

var = Outer[ψ, grid, grid];

sol = 
   FindRoot[{ae, aebc} /. Etr -> 1, {#, 1} & /@ Flatten@var]; // AbsoluteTiming
(* {0.365270, Null} *)

ListPlot3D[var /. sol, PlotRange -> All, DataRange -> X]

Mathematica graphics

Notice setting proper initial guess in FindRoot can be troublesome, but once again, fortunately your equation seems not to be the case.

I guess the FindRoot result could be used to creat an InterporlatingFunction that could be fed to another NDSolve later, correct? — ivbc, May 26 '17 at 15:38
@ivbc Yes, just use e.g. solfunc = ListInterpolation[var /. sol, {{-X, X}, {-X, X}}] — xzczd, May 26 '17 at 15:45
I will wait a bit more to accept the answer. The pdetoae function is taking a bit for me to understand and I would like to see if someone comes up with a simpler method. — ivbc, May 29 '17 at 16:54
@ivbc Feel free to wait :) . Hope "FiniteElement" will support nonlinear equations soon. — xzczd, May 30 '17 at 03:18

Getting strange "not a polynomial" error from NDSolve

1 Answers1

Linked