How can I plot eigenvalues?

Question

B[t_] = {
  {i*x_ {1}/2, J_ {1}, 0, g_ {1}*a_ {1}, 0},
  {J_ {1}, i*x_ {2}/2, J_ {2}, -g_ {1}*a_ {2}, g_ {2}*a_ {2}}, {0, 
   J_ {2}, i*x_ {3}/2, 
   0, -g_ {2}*a_ {3}}, {g_ {1}*a_ {1}, -g_ {1}*a_ {2}, 0, i*y_ {1}/2, 
   0}, {0, g_ {1}*a_ {2}, -g_ {1}*a_ {3}, 0, i*y_ {2}/2}
  }

where J_{1}=J_{2}=1/2, a_{3} = 30*Exp[-(t)^2/t_{1}], a_{2}=0, a_{1} = 30*Exp[-(t - t_{0})^2/t_{1}], t_{0} and t_{1} are constant, g_{1} = g_{2}=0.01, x_{i}=y_{i}=0 for simplest case and later may be taken arbitrary.

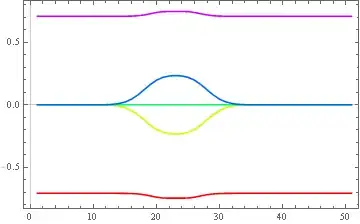
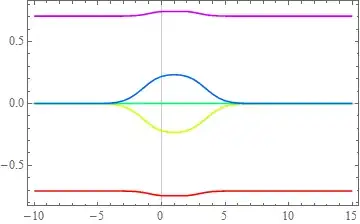
I want to plot the eigenvalues.

I have used following command but axis label is not varying correctly.

data = Table[Eigenvalues[B[t/2]], {t, -10, 15, 0.5}]; 

ListPlot[Transpose[Sort /@ data], Frame -> True, FrameStyle -> Directive[Black, 12]]

please let me know how can I plot eigenvalues with time t long x-axis and what about if x_{i}=y_{i} are non zeros.

You just edited your question, not to fix the number of errors in it, but to ask for extra features not present in the original post. You are shifting the goalpost. It's frustrating to contribute effort to a specific question to then receive contradictory details or new requests not mentioned in the original request. You make the work others have done on your behalf seem irrelevant. Mma.SE is not a private consulting service but a public Q&A forum. Please, out of respect to the people trying to help you, either ask the question you need to ask properly the first time, or ask a new question. — rhermans, May 28 '17 at 09:43
Dear rhermans, I apologize that I edit the question. Because I found that plots are similar that I had already and as I mentioned that label are not correct. but forgot to mention the time scale. I will keep your words in mind. thanks — Ani, May 28 '17 at 11:51
@Anilchauhan, I have edited the question to include what you need. There is further to discuss , please go to this chat room (follow the link) — rhermans, May 30 '17 at 10:23

rhermans · Answer 1 · 2017-05-30T10:48:16.363

Start by writing things in Wolfram Mathematica Language, something like this

B[t_] = With[{t0 = 1, t1 = 1},
  With[{
    J1 = 1/2,
    J2 = 1/2,
    a3 = 30*Exp[-(t)^2/t1],
    a2 = 0,
    a1 = 30*Exp[-(t - t0)^2/t1],
    g1 =  0.01, g2 = 0.01,
    x1 = 0, x2 = 0, x3 = 0,
    y1 = 0, y2 = 0
    }, {
    {i*x1/2, J1, 0, g1*a1, 0},
    {J1, i*x2/2, J2, -g1*a2, g2*a2},
    {0, J2, i*x3/2, 0, -g2*a3},
    {g1*a1, -g1*a2, 0, i*y1/2, 0}, 
    {0, g1*a2, -g1*a3, 0, i*y2/2}
    }]]

This can't be put into ListPlot, unless you define values for t1 and t2, so I did.

Now this gives an array of {51, 5} numbers that you will need to Flatten, or Sort and Transpose

ListPlot@Flatten@Table[
   Eigenvalues[B[t/2]]
, {t, -10, 15, 0.5}]

ListPlot[
 Transpose@Table[
   Sort[Eigenvalues[B[t/2]]], {t, -10, 15, 0.5}]
 , PlotStyle -> Array[Hue, 5, {0, 0.8}]
 , Joined -> True
 , PlotTheme -> "Scientific"
 ]

Mathematica graphics

Scaled

ListPlot[
 Transpose@Table[
   {t, #} & /@ Sort[Eigenvalues[B[t/2]]]
   , {t, -10, 15, 0.5}
   ]
 , PlotStyle -> Array[Hue, 5, {0, 0.8}]
 , Joined -> True
 , PlotTheme -> "Scientific"
 ]

Dear rhermans, thanks for the corrections. But I want time t along x-axis. how can I do it? — Ani, May 28 '17 at 09:16
@Anilchauhan, next time, you should show more effort from your side before asking. We volunteer our time to give general help to people, this is not a free coding and debugging service. Your future good questions are welcome. Learn about common pitfalls here. Please visit the links. — rhermans, May 28 '17 at 09:39

How can I plot eigenvalues?

1 Answers1

Scaled