Counting number of spheres that contain a point

Question

I have created this set of spheres in Mathematica.

The code I used to produced this is as follows:

satnum=Input["Select Number of Satellites"]
alt=Input["Select an orbit altitude (km)"]
sensorstr=Input["Select sensor strength (km)"]
Graphics3D[{Opacity[1],Sphere[{0,0,0},6371]}]
spacing=2pi/(satnum)
angles=-Range[-pi,pi-.000000001,spacing]
radius=ConstantArray[6371+alt,satnum]
centroids=Transpose[{radius,angles}]
cartcentroids=FromPolarCoordinates[centroids]
zdim=ConstantArray[0,satnum]
cartcentroids=Transpose[{cartcentroids,zdim}]
cartcentroids=Flatten[cartcentroids]
cartcentroids=Partition[cartcentroids,3]
Graphics3D[{Sphere[cartcentroids,sensorstr],Opacity[.2],Sphere[{0,0,0},7571]}]

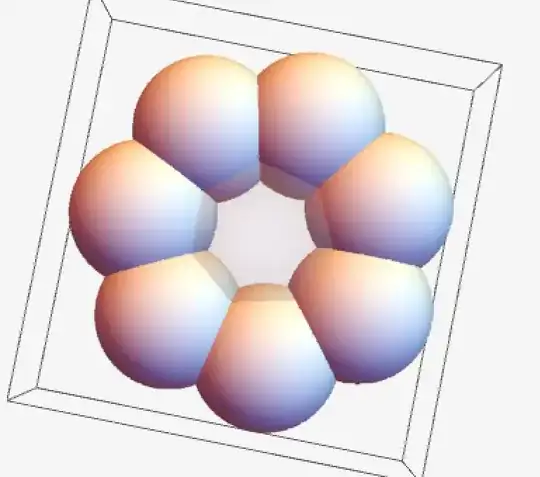
Basically I want to draw a circle of a given radius r around the transparent sphere in the middle and count how many solid spheres contain a point at a given angle (once a starting point is defined). In this case the # of containing spheres would always be 1 or 2 as long as the circle has a small enough radius. I've looked into functions such as RegionIntersection or Surface Intersection, but I can't seem to figure out exactly how I should approach this problem.

Thanks for any help.

If you can give examples of your code this could help others? — Dunlop, Jun 14 '17 at 20:11
at least partly answered here: https://mathematica.stackexchange.com/questions/79524/how-to-draw-a-circle-in-3d-on-a-sphere — george2079, Jun 14 '17 at 20:22
Look at RegionMember. You should simply check if a given point is a member of each of the spheres. — yohbs, Jun 14 '17 at 20:23
Looks like I could put together a solution using RegionMember, thanks @yohbs — Evan, Jun 14 '17 at 20:38

score 3 · Accepted Answer · answered Jun 14 '17 at 20:38

So the core of the problem is to determine of a point intersects a region. A Sphere is hollow, a Ball is solid, so you want Ball. Example here...

bunchofballs = Table[Ball[{x, 0, 0}], {x, 0, 4}]

Show[Graphics3D[bunchofballs]]

Now count intersections for a point p={1,0,0}

Count[Map[RegionMember[#, p] &, bunchofballs], True]

(*  3  *)

score 2 · Answer 2 · answered Jun 14 '17 at 21:31

MikeY's solution is the right thing to do in the general case. In the case of spheres you can gain a lot of computation time by checking directly if the distance to the sphere center is smaller than the radius. Here's a comparison for 10000 spheres:

(*set up the spheres:*)
n = 10000;
radii = RandomReal[{0.5, 1.5}, n];
centers = RandomReal[{0, 10}, {n, 3}];
bunchofballs = Table[Ball[centers[[i]], radii[[i]]], {i, n}];
(*see how many spheres contain p0:*)
p0 = RandomReal[{0, 10}, 3];
AbsoluteTiming@Count[Map[RegionMember[#, p0] &, bunchofballs], True]
AbsoluteTiming@ Count[Table[Norm[p0 - centers[[i]]] < radii[[i]], {i, n}],True]
(*Output:
{4.75374, 28}
{0.038338, 28}
*)

That's a 100 times faster.

Counting number of spheres that contain a point

2 Answers2