7

Color mixing seems not only one type.

Here is RGB_color_model

I wrote this one:

coord = 1/2*{{1, -Sqrt[3]/3}, {0, 2 Sqrt[3]/3}, {-1, -Sqrt[3]/3}};
color = {Red, Green, Blue};
MapThread[
  Graphics[{##}, PlotRange -> 2, Background -> Black] &, {color, 
   Disk /@ coord}];
Plus @@ (ImageData /@ %) // Image
Clear[coord, color]

enter image description here

Another type of mixing is :

{#, Graphics[{#, Disk[]}, ImageSize -> 50]} & /@ 
 DeleteDuplicates[Blend /@ Permutations[{Red, Blue, Green}, {2}]]

enter image description here

So How can I get the following like this ?

enter image description here

chyanog
  • 15,542
  • 3
  • 40
  • 78

2 Answers2

12

Although kguler correctly yields the picture that you set as a goal here I wonder whether this really is what is behind the question.

You mention another type of mixing and since you start with an example of additive mixing of the RGB primaries I feel you may have the intention to deal with subtractive mixing of colors.

The primary colors of subtractive mixing, the type of mixing that deals with paints and printed colors, are Yellow, Cyan, and Magenta:

{#, Graphics[{#, Disk[]}, ImageSize -> 50]} & /@ {Yellow, Magenta, Cyan}

Mathematica graphics

The colors you provided are just murkier versions of them (you used 1/2's instead of 1's).

You can see Cyan, Magenta, and Yellow as "negative" Red, Green and Blue respectively. Using a slightly changed version of your code:

coord = 1/2*{{1, -Sqrt[3]/3}, {0, 2 Sqrt[3]/3}, {-1, -Sqrt[3]/3}};
color = {Red, Green, Blue};
circles = MapThread[Image[Graphics[{##}, PlotRange -> 2, Background -> Black], 
    ImageSize -> 300] &, {color, Disk /@ coord}]

ImageSubtract[Image[ConstantArray[{1, 1, 1}, {300, 300}], "Real"], #] & /@ circles // Row

Mathematica graphics

Using that, you can now easily crate the three overlapping circles of subtractive color mixing.

Fold[ImageSubtract,Image[ConstantArray[{1, 1, 1}, {300, 300}], "Real"], circles]

Mathematica graphics

Sjoerd C. de Vries
  • 65,815
  • 14
  • 188
  • 323
  • 1
    ColorNegate[img] gives the same result? (where img is the first image in OP's question) – kglr Nov 18 '12 at 14:29
  • @kguler Yes, but I found it more instructive to build it up as three separate subtractions. It gets you closer to the process that is subtractive mixing. – Sjoerd C. de Vries Nov 18 '12 at 15:41
7

Update 2:

Use ImageApply to replace the channel values of each pixel with the values that correspond to blended values:

img=Image[Plus @@ (ImageData /@ MapThread[Graphics[{##}, PlotRange -> 2, 
  Background -> Black] &,  {color,  Disk /@ coord}])];
ImageApply[If[Tr[#] == 0, #, #/Tr[#]] &, img]

or, better yet, (courtesy of J.M.) 

ImageApply[Normalize[#, Tr] &, img]

enter image description here

Update 1:

Post-process the original image to replace intersection colors with the blended versions:

ImageData[img] /.  {{1., 1., 1.} -> {1./3, 1./3, 1./3},
    {1., 1., 0.} -> {1./2, 1./2, 0.},
    {0., 1., 1.} -> {0., 1./2, 1./2},
    {1., 0., 1.} -> {1./2, 0., 1./2}} // Image

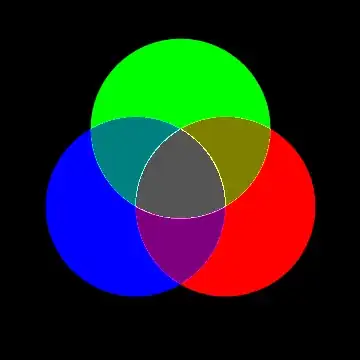
enter image description here

Original post:

You can use RegionPlot to get a picture with circle intersections colored using Blend:

circles = (0 <= (x - #[[1]])^2 + (y - #[[2]])^2 <= 1) & /@ coord;
subregions =  Most@(And @@ # & /@ (Thread[{#, circles}] & /@ 
   Tuples[{Identity, Not}, Length@circles] /. {x_, y_} :> x[y]));
subregioncolors = Thread[{#, color}] & /@
     Tuples[{Identity, # /. # -> Sequence[] &}, Length@color] /.
        {x_, y_} :> x[y] /. {} -> Sequence[];
subregioncolors = Map[Blend@Flatten@{#1, #1} & , subregioncolors];
RegionPlot[subregions, {x, -2, 2}, {y, -2, 2},
    PlotStyle -> subregioncolors, BoundaryStyle -> White,
    PlotPoints -> 150, Background -> Black]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896