Generating random points on a Klein's bottle

Question

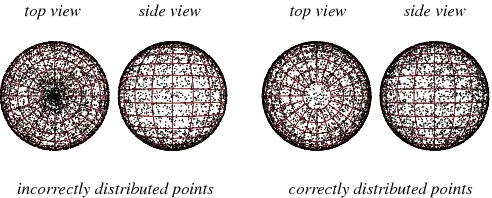
There is a neat way in Mathematica to generate random points on a sphere. Note that "randomness" is defined (somewhat not mathematically strictly) so that the points must be evenly distributed over the sphere (see more info in the linked demo):

Is there a similar (or even very different but reasonable) way of generating random points on Klien's bottle?

klein[u_, v_] := Module[{
   bx = 6 Cos[u] (1 + Sin[u]),
   by = 16 Sin[u],
   rad = 4 (1 - Cos[u]/2),
   X, Y, Z},
  X = If[Pi < u <= 2 Pi, bx + rad Cos[v + Pi], bx + rad Cos[u] Cos[v]];
  Y = If[Pi < u <= 2 Pi, by, by + rad Sin[u] Cos[v]];
  Z = rad Sin[v];
  {X, Y, Z}
  ]

ParametricPlot3D[klein[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi}, Axes -> False, Boxed -> False]

(code and image courtesy of @e.doroskevic)

@whoever cast that vote: You're kidding, surely; a close vote due to "a simple mistake"? maybe a dupe, but I'll give it the benefit of the doubt for now. — LLlAMnYP, Jun 20 '17 at 10:14

score 14 · Answer 1 · answered Jun 19 '17 at 18:35

14

There is a function for this since Mathematica 10.2.

graphics = ParametricPlot3D[
   klein[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi},
   Axes -> False,
   Boxed -> False
   ];

reg = DiscretizeGraphics[graphics];
pts = RandomPoint[reg, 1000];

Show[
 graphics,
 Graphics3D[Point[pts]]
 ]

Mathematica graphics

answered Jun 19 '17 at 18:35

C. E.

70,533
6
140
264

Thanks, but I am not convinced that the points are uniformly distributed on the surface. – VividD Jun 19 '17 at 18:47
1

Why not? and what would convince you? – yohbs Jun 19 '17 at 18:59
@VividD The documentation explicitly says that "RandomPoint will generate points uniformly in the region reg." – C. E. Jun 19 '17 at 19:06
I suspect the points generated by RandomPoint will be obtained by applying uniform distribution for parameters - however, this will NOT distribute points evenly on the surface, in case of Klein's bottle. @yohbs – VividD Jun 19 '17 at 19:28
@C.E. It doesn't seem to me that DiscretizeGraphics generate reg that will result in even distribution of points on the surface. – VividD Jun 19 '17 at 19:30
2

Well, your suspicion is unsubstantiated. RandomPoint generates uniform distribution in the embedding space, not in the coordinate space. That's the sole point of having this function. – yohbs Jun 19 '17 at 19:31
@yohbs But your embedding space may be wrong. – VividD Jun 19 '17 at 19:32
Sorry, I just don't get what you're saying. Can you show why it seems to you that it's wrong? Can you give any demonstration that it is not uniform? Unless you do so, there's really no point in debating this. – yohbs Jun 19 '17 at 19:34
I am asking the question, I should expect you to give me the proof of correctness, not vice versa. @yohbs – VividD Jun 19 '17 at 19:40
12

Well, that's both rude, disrespectful and ungrateful. You asked a question showing zero effort, got an answer saying that what you're looking for is a built in function, expressed unsubstantiated doubts about the implementation of this function, again showing zero effort in supporting your claim nor gratitude for @C.E. For taking the time to answer you, and now you expect us to provide a proof of correctness? Why on earth do you think that someone will do that for you? – yohbs Jun 19 '17 at 19:52
No, @yohbs the basics of science is to raise doubts and ask for proofs. – VividD Jun 19 '17 at 20:01
5

You can ask as many questions and raise as many doubts as you want. The basics of etiquette is to show some effort if you want other people to do stuff for you. – yohbs Jun 19 '17 at 20:19
5

Validating the actually uniformity of the RandomPoint distribution should be a new question (The question isn't really specific to the Klein bottle is it?). Of course if you pose the question you should show some thought as to how to approach it. – george2079 Jun 19 '17 at 20:47
2

I want to see the algorithm and proof-of-correctness as much as anybody, but this is Mathematica Stack Exchange, not Mathematics Stack Exchange. I think the more general question might be a better fit there, not here - I would only expect the name of a built-in function here unless the question was specifically about implementation details. – Darren Jun 19 '17 at 23:18
I don't see Mathematica Stack Exchange as "somebody doing work for someone else" at all but as a free intellectual playground where we can together ask and answer and discuss, and be rewarded by the knowledge. But, @yohbs obviously does not share my view, that is his right too, what can I do. – VividD Jun 20 '17 at 05:13
4

@VividD RandomPoint does sample uniformly over a region. In fact here's a blog post about RandomPoint where in the first paragraph the author talks about how sampling over the parameters of a sphere does not give a uniform sample in this sense. http://blog.wolfram.com/2015/11/13/new-in-the-wolfram-language-randompoints/ – Greg Hurst Jun 20 '17 at 05:27
@ChipHurst Yes, an excellent link, thanks. – VividD Jun 20 '17 at 05:39

george2079 · Accepted Answer · 2017-06-20T18:24:06.253

Here's how you do from first principles. I'd assume this is just what RandomPoint does internally.

compute surface incremental area associated with an area increment in parameter space:

del = 0.01;
da[u_?NumericQ, v_?NumericQ] :=
 Module[{uu, dd},
  uu = Clip[ # + del {-1, 1}, {0, 2 Pi}] & /@ {u, v}; 
  dd = Times @@ Subtract @@@ uu;
  Norm@Cross[
     klein[uu[[1, 2]], v] - klein[uu[[1, 1]], v],
     klein[u, uu[[2, 2]]] - klein[u, uu[[2, 1]]]]/dd ]

(The derivatives could be done analytically here but it takes a bit of hand work due to the If embedded in klein )

In principle if you normalize da you have a 2D PDF , unfortunately RandomVariate cant handle a 2d distribution RandomVariate from 2-dimensional probability distribution so we brute force it here.. ( I'm sure there is a cleaner way to do this, but it gets the job done. )

np = 5000;
rp = klein @@@ (RandomSample[(da @@@ #) -> #, np] &@
     RandomReal[{0, 2 Pi}, {50 np, 2}]);

Show[{
  ParametricPlot3D[klein[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi}, 
   Axes -> False, Boxed -> False, PlotStyle -> Opacity[.5], 
   Mesh -> None],
  Graphics3D[{Red, Point[rp]}]}]

Here's an exact expression for the surface incremental area: Norm[Cross[{6 Cos[u]^2 - 2 Sin[u] (3 + Cos[v] + 3 Sin[u]) + 2 Cos[v] (Sin[2 u] - Sin[u]) UnitStep[π - u], 16 Cos[u] - 2 (Cos[2 u] - 2 Cos[u]) Cos[v] UnitStep[π - u], 2 Sin[u] Sin[v]}, {2 (Cos[u] - 2) Sin[v] ((1 + Cos[u]) UnitStep[π - u] - 1), 2 (Cos[u] - 2) Sin[u] Sin[v] UnitStep[π - u], 2 (2 - Cos[u]) Cos[v]}]] — J. M.'s missing motivation, Aug 06 '17 at 14:21

Generating random points on a Klein's bottle

2 Answers2