12

I'm working with a list of lists (a large table).

How would I extract the first 9 rows from every 22 rows of this list?

Essentially, I'd like to drop rows 10 to 22, and then 32 to 44, and so on, repeated until the end of the data.

For example, I'd like to turn this:

data = {{1,1,1},{2,2,2},{3,3,3},{4,4,4},{5,5,5},{6,6,6},{7,7,7},{8,8,8},
{9,9,9},{10,10,10},{11,11,11},{12,12,12},{13,13,13},{14,14,14},{15,15,15},
{16,16,16},{17,17,17},{18,18,18},{19,19,19},{20,20,20},{21,21,21}, 
{22,22,22},{23,23,23}}

Into:

{{1,1,1},{2,2,2},{3,3,3},{4,4,4},{5,5,5},{6,6,6},{7,7,7},{8,8,8},
{9,9,9},{23,23,23} (*and so on*)}

I am a beginner at Mathametica--please forgive me if this is a repeat question.

Many thanks.

andre314
  • 18,474
  • 1
  • 36
  • 69
musicmaker
  • 121
  • 3

4 Answers4

14

You can use Partition with a suitable offset:

Partition[Range[100], 9, 22]

{{1, 2, 3, 4, 5, 6, 7, 8, 9}, {23, 24, 25, 26, 27, 28, 29, 30, 31}, {45, 46, 47, 48, 49, 50, 51, 52, 53}, {67, 68, 69, 70, 71, 72, 73, 74, 75}, {89, 90, 91, 92, 93, 94, 95, 96, 97}}

As some have pointed out, this solution needs to be slightly modified if "overhang" is desirable. WReach notes that one can use

Partition[data, UpTo[9], 22]

for this case in Mathematica 10.3 and later.

C. E.
  • 70,533
  • 6
  • 140
  • 264
  • 8
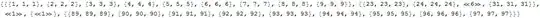
    The complete answer should be Flatten[Partition[data, 9, 22, {1, 1}, {}], 1] – swish Jun 24 '17 at 21:15
  • To see where are the problems without the ...{1,},{}] try Partition[Range[115], 9, 22,{1,1},{}]and compare to Partition[Range[125], 9, 22] – andre314 Jun 24 '17 at 21:21
  • 6
    +1. From Mathematica 10.3 onwards we can write Partition[data, UpTo[9], 22] if we want to keep any "dangling" elements at the end of the list. – WReach Jun 24 '17 at 21:29
  • Works perfectly. Thanks very much C.E., andre, swish, and WReach. – musicmaker Jun 24 '17 at 21:31
  • 1
    @swish It wasn't clear from the question that there could be overhang, but good point in any case. – C. E. Jun 24 '17 at 22:38
9

you can do : 

ReplacePart[data,{i_ /; Mod[i-1,22]>8}-> Nothing]

{{1, 1, 1}, {2, 2, 2}, {3, 3, 3}, {4, 4, 4}, {5, 5, 5}, {6, 6, 6}, {7, 7, 7}, {8, 8, 8}, {9, 9, 9}, {23, 23, 23}}

Edit

Here is a more understable syntax, specially for beginners: 

Table[If[Mod[i-1,22]>8,Nothing,data[[i]]],{i,1,Length[data]}]
andre314
  • 18,474
  • 1
  • 36
  • 69
5
n = 100;
o = 22;

data = Table[{i, i, i}, {i, 100}];

pos = NestList[# + o &, {1, 9}, Floor[n/o]]

{{1, 9}, {23, 31}, {45, 53}, {67, 75}, {89, 97}}

data[[#1 ;; #2]] & @@@ pos // Short (* thanks Mr. Wizard *)

enter image description here

eldo
  • 67,911
  • 5
  • 60
  • 168
5
#[[Flatten[Range[Range[9], Length@#, 22], {2,1}]]]& @ data

{{1, 1, 1}, {2, 2, 2}, {3, 3, 3}, {4, 4, 4}, {5, 5, 5}, {6, 6, 6},
{7, 7, 7}, {8, 8, 8}, {9, 9, 9}, {23, 23, 23}}

kglr
  • 394,356
  • 18
  • 477
  • 896
  • It is an order of magnitude faster to use Transpose rather than Sort, i.e. Catenate[Range[Range[9], n, 22]\[Transpose]]. By the way this is essentially f5 from https://mathematica.stackexchange.com/a/21220/121. I need to compare Transpose and Flatten however. Edit I guess I used Flatten to handle ragged lists. – Mr.Wizard Jun 28 '17 at 12:29
  • @Mr.Wizard, Catenate[Range[Range[9], n, 22]\[Transpose]] gives an error message (The first two levels of {{1,23},{2,24},{3},{4},{5},{6},{7},{8},{9}} cannot be transposed). I updated with an alternative way to avoid Sorting. – kglr Jun 28 '17 at 12:38
  • Yeah, I realized that pretty quickly. Now your answer is exactly f5, excluding syntax. – Mr.Wizard Jun 28 '17 at 12:39
  • @Mr.Wizard, right re f5. Makes me feel proud:) – kglr Jun 28 '17 at 12:44
  • That's very generous, as you surely know I have learned a lot from you. – Mr.Wizard Jun 28 '17 at 13:33