Basins of attraction when using Newton's method to solve $x^3-1 = 0$

Question

I created Newton fractal plot for x^3 - 1 and would like to know where did I go wrong. I know I could have just copied the code but that would not have been fun.

x = N[FindDivisions[{-2, 2}, 200], 8];
y = N[FindDivisions[{-2, 2}, 200], 8];
fx = xn^3 - 1;
f1x = 3*xn^2;
r = {};
r2 = {};
r3 = {};

i = 1;
j = 1;
iter = 1;
For[i = 1, i < 200,
 xi = x[[i]];
 For[j = 1, j < 200,
   yi = y[[j]];
   xn = xi + I*yi;
   For[iter = 1, iter < 7,
     xn1 = N[xn - fx/f1x, 8];
     xn = xn1;
     iter++;
     ]
    Which[Im[xn] < 0`10, AppendTo[r, {x[[i]], y[[j]]}], Im[xn] > 0`10,
       AppendTo[r2, {x[[i]], y[[j]]}], Im[xn] == 0`10, 
     AppendTo[r3, {x[[i]], y[[j]]}]]
    j++;
   ]
  i++;]

a = ListPlot[r, PlotStyle -> Red];
b = ListPlot[r2, PlotStyle -> Blue];
c = ListPlot[r3, PlotStyle -> Green];
Show[a, b, c]

As you can see it looks similar but not exactly like the required one. Would like to know what I can do to make it better. Should I increase the number of test cases? Would it help?

You write: "As you can see it looks similar but not exactly like the required one. ". No, I can't see that as you supply no "required one" to compare it to. — m_goldberg, Jun 27 '17 at 01:58
Hint. Your use of arbitrary precision arithmetic at low precision is not speeding up your code. Machine arithmetic is always the fastest way to compute. — m_goldberg, Jun 27 '17 at 14:28
More hints: Your For-loop syntax is incorrect -- your iterator increments should be given as the 3rd argument to For. You are a missing the semi-colon needed to separate your Which expression from For-loop that precedes it. — m_goldberg, Jun 27 '17 at 15:03
how to located three roots in the second picture. could you tell me how does it make in matlab? — onk, Feb 22 '18 at 09:06

score 10 · Answer 1 · answered Jun 27 '17 at 08:28

Just to illustrate avoidance of For loop, use of MatrixPlot (requires change of representation):

f[z_] := z - (z^3 - 1)/(3 z^2)
roots = {{1, 0}, {-1/2, Sqrt[3]/2}, {-1/2, -Sqrt[3]/2}};
nt[x_, y_, n_] := 
 FixedPoint[f[Complex @@ #] &, {x, y}, n] /. Complex[a_, b_] :> {a, b}
cfn[x_, y_, n_] := 
 With[{r = nt[x, y, n]}, Which[Norm[r - {1, 0}] < 10^(-6), 1,
   Norm[r - {-1/2., Sqrt[3]/2.}] < 10^(-6), 2, 
   Norm[r - {-1/2., -Sqrt[3]/2.}] < 10^(-6), 3]]
Legended[MatrixPlot[
  Reverse@Transpose@
    Table[cfn[i, j, 40], {i, -2, 2, 0.015}, {j, -2, 2, 0.015}], 
  DataRange -> {{-2, 2}, {-2, 2}}, 
  ColorRules -> {1 -> Red, 2 -> Green, 3 -> Blue}, 
  Epilog -> {Yellow, PointSize[0.02], Point[roots]}], 
 SwatchLegend[{Red, Green, Blue}, Style[#1 + #2 I, 20] & @@@ roots]]

score 4 · Answer 2 · edited Jun 16 '20 at 09:23

You need a lot more iterations at a lot more points to get a good image of the basins of attraction. With a faster implementation than yours, I was able to get a reasonably good image when iterating 15 times at 250,000 points (500 x 500 lattice).

I also think your code may have bugs that are distorting the image, so I'm not sure you will get a correct image even if you increase the number of iterations and use more points.

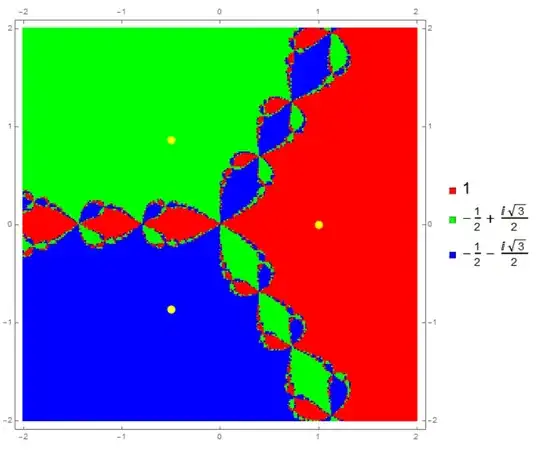
This is the image my code produces.

Update

I have two sets of code that can generate the above image. The 1st is a repaired and speeded up version of the OP's code. I don't recommend using this code, but it might be instructive to the OP and others to see what is more or less the minimum needed to make the posted code work.

fx[u_] := u^3 - 1;
f1x[u_] := 3 u^2;
n = 500;
y = x = Subdivide[-2., 2., n];
max = 15;
r1 = r2 = r3 = r[];
For[i = 1, i <= n + 1, i++,
  xi = x[[i]];
  For[j = 1, j <= n + 1, j++,
    xn = xi + I*y[[j]];
    Quiet @ 
      For[iter = 1, iter < max, iter++,
        xn1 = xn - fx[xn]/f1x[xn];
        xn = xn1];
    imxn = Im[xn];
    Which[
      imxn == 0., r3 = r[{x[[i]], y[[j]]}, r3],
      imxn < 0., r1 = r[{x[[i]], y[[j]]}, r1],
      imxn > 0., r2 = r[{x[[i]], y[[j]]}, r2]]]]

Accumulating the deeply nested r expressions is much faster than the AppendTos the OP was using to accumulate basin points. This is a major speed boost.

We must flatten the results afterward, but that too is fast.

pts = List @@@ (Flatten @* r /@ {r1, r2, r3});
a = ListPlot[pts[[1]], PlotStyle -> Blue];
b = ListPlot[pts[[2]], PlotStyle -> Yellow];
c = ListPlot[pts[[3]], PlotStyle -> Red];
Show[a, b, c,
  Axes -> None,
  AspectRatio -> Automatic,
  ImageSize -> Large]

The 2nd code set is the one I recommend. This, in essence, remains a straight-forward translation of OP's code, preserving the the basic procedural approach, but replacing elements of what I consider bad practice with code that is widely accepted as good practice. Note that I do not introduce any global variables. Only the function definitions are made at top-level.

fx[u_] := u^3 - 1;
f1x[u_] := 3 u^2;
With[{n = 500, max = 15},
  pts =
    Module[{x, b, b1, b2, b3, root, yRoot},
      x = Subdivide[-2., 2., n];
      b3 = b2 = b1 = b[];
      Do[
       root = Quiet @ Nest[# - f[#]/df[#] &, x[[i]] + I x[[j]], max];
       yRoot = Im[root];
       Which[
         yRoot == 0., b1 = b[{x[[i]], x[[j]]}, b1],
         yRoot < 0., b2 = b[{x[[i]], x[[j]]}, b2],
         yRoot > 0., b3 = b[{x[[i]], x[[j]]}, b3]],
      {i, n + 1}, {j, n + 1}];
    List @@@ (Flatten @* b /@ {b1, b2, b3})]];

Do and Nest are faster than For, and only one Do expression is needed. Further, since the point lattice being constructed is the same in both directions, only one list of divisions is needed.

ListPlot[{pts[[1]], pts[[2]], pts[[3]]},
  PlotStyle -> {Red, Blue, Yellow},
  Axes -> None,
  AspectRatio -> Automatic,
  ImageSize -> Large]

Show is not needed.

@user49702. What are you asking me to share? Your "it" is a pronoun with no reference — m_goldberg, Jun 27 '17 at 14:31
Perhaps, the OP is referring to the code you used to produce your plot. — bbgodfrey, Jun 27 '17 at 15:13
@bbgodfrey. Probably. But it is not perfectly clear and I think it should be. I don't want to make an effort only to be told what I posted wasn't what was asked for. (Happened to me more than once already) — m_goldberg, Jun 27 '17 at 15:32
@user49702. I am willing to post my code if you will confirm that is what you are asking me to do. — m_goldberg, Jun 27 '17 at 15:40
I am asking you to post the code you used to generate the fractal you produced. Thanks — user49702, Jun 28 '17 at 05:31
update: I wanted to expand the code for 2 point methods like Jarratt or Ostrowski type methods, is it possible? I tried but the execution time is quite long for that program. — user49702, Jul 10 '17 at 02:05
@user49702. That is a whole new question and should not be addressed to me in a comment. It should be posted as new question for whole community to see. — m_goldberg, Jul 10 '17 at 03:11

Basins of attraction when using Newton's method to solve $x^3-1 = 0$

2 Answers2

Update