Precision of FindRoot output doesn't match input

Question

EDIT: I just realized this is closely related to a question I asked two years ago, Is FindRoot wrong about its WorkingPrecision? (which is still unanswered). I don't know if the current question counts as a duplicate, but it may ask the same thing more clearly. I hope you still read this one and see if the different phrasing triggers any insights.

I have a similar question as Precision of FindRoot but slightly different. Consider getting an InterpolatingFunction f[t] from NDSolve then finding a root with FindRoot:

Clear[f]
fsol = NDSolve[{f''[t] - f'[t] + f[t] - 1 == 0, f[0] == 1, 
    f'[0] == 1}, f, {t, 0, 20}, WorkingPrecision -> $MachinePrecision];
f[t_] = Evaluate[f[t] /. fsol];

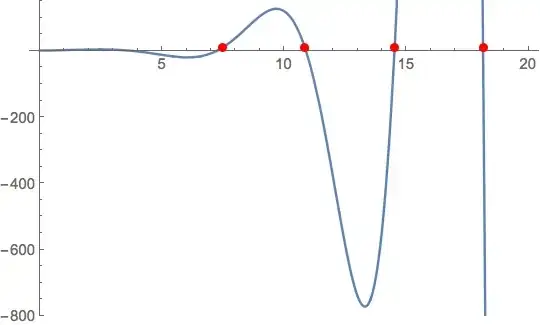
Plot[f[SetPrecision[t, Infinity]], {t, 0, 20}, PlotRange -> All]

t0 = t /. FindRoot[f[t] == 10, {t, 18}, WorkingPrecision -> 50]
Precision@f[t0]
Precision@t0

Output:

18.136956334574359755720315216764489747727661914414

11.6327

50.

The precision of my root t0 is equal to the WorkingPrecision I gave in FindRoot, despite that that is higher than the Precision of f itself, which came from NDSolve. My intuition about precision as a concept may be failing me here, but this does not seem right. My hunch is that if you use FindRoot to solve f[t]==number, then your answer for t should be no more precise than the precision of f at that t.

Even if Mathematica is technically right (is it?), I feel it's failing my purposes. There's real error introduced by the imprecision of my f[t]. Once I get t0 and plug it in (in my actual code it won't be back into f[t]!), I want it to reflect that t0 is imprecise because it was solving for an f[t] that was imprecise.

So I'd like answers to (a) Is Mathematica misusing precision here? And if not, then (b) Is there a way to make it reflect precision in a way that seems honest to me?

Answer 1

This doesn't answer your question but rather notes that the differential equation can be solved exactly.

Clear[f]

eqns = {f''[t] - f'[t] + f[t] - 1 == 0, f[0] == 1, f'[0] == 1};

fsol = DSolve[eqns, f, t][[1]];

Verifying that the solution satisfies the equations

eqns /. fsol // Simplify

(*  {True, True, True}  *)

f[t_] = f[t] /. fsol // Simplify

(*  1 + (2*E^(t/2)*Sin[(Sqrt[3]*t)/2])/
     Sqrt[3]  *)

There are four solutions for f[t] == 10. These can all be found using NSolve (or Solve or Reduce) rather than FindRoot

f10 = t /. NSolve[{f[t] == 10, 0 < t < 20}, t, Reals,
   WorkingPrecision -> 50]

(*  {7.4711859387099462515468807380311790899637056073604, \
10.843003786966755891571562660309141693335994867762, \
14.516733262382665885039289324062217368693394531490, \
18.136956466215141134109455148326120335487744137331}  *)

Plot[f[t], {t, 0, 20}, PlotRange -> {-800, 150},
 Epilog -> {Red, AbsolutePointSize[6],
   Point[{#, 10} & /@ f10]}]

Precision /@ f10

{50., 50., 50., 50.}

However, some precision is lost in calculating the function

f /@ f10

(*  {10.00000000000000000000000000000000000000000000000, \
10.0000000000000000000000000000000000000000000000, \
10.000000000000000000000000000000000000000000000, \
10.00000000000000000000000000000000000000000000}  *)

Precision /@ %

(*  {48.4669, 47.602, 46.6845, 45.8028}  *)

The precision decreases with increasing magnitude of the first derivative of f

Abs[f'[#]] & /@ f10 // N

(*  {45.6818, 221.584, 1424.41, 8672.91}  *)