Li = Range[5];
TakeDrop[Li, #] & /@ Range[Length[Li]-1] // Column[Row/@#]&
or, slightly shorter,
i = 1; TakeDrop[Li, i++] & /@ Most[Li] // Column[Row/@#]&
or, using just Range and organizing the result with Transpose:
Transpose[{Range[Range[4]], Range[1 + Range[4], 5]}] // Column[Row/@#]&

For an arbitrary list of size 5, say, lst = {w, v, x, y, z},
lst[[#]] & /@ # & /@ Transpose[{Range[Range[4]], Range[1 + Range[4], 5]}] // format

A few more alternatives:
ClearAll[f1, f2, f3, f4, f5, f6, f7, f8, f9, f10, ☺]
f1 = Module[{i = 1, lst = #}, TakeDrop[lst, i++] & /@ Rest[lst]] &;
f2 = Module[{lst = #}, TakeDrop[lst, #] & /@ Range[Length[lst] - 1]] &;
f3 = Table[Partition[#, Length@#, 1, {-1, 1}, {}][[{i, i + Length@#}]], {i, Length@# - 1}]&
f4 = Module[{lst = #, l = Length@# - 1}, lst[[#]] & /@ # & /@
Transpose[{Range[Range[l]], Range[1 + Range[l], l + 1]}]] &;
f5 = Module[{lst = #, r = Range[Length[#] - 1], l = Length@#, parts},
parts =Transpose[{Range[r], Range[1 + r, l]}]; Extract[lst, List/@ #] &/@ parts]&;
f6 = Function[{x}, Most@MapIndexed[{x[[;; #2[[1]]]], x[[1 + #2[[1]] ;;]]} &, x]];
f7 = Table[Values@GroupBy[MapIndexed[{#2[[1]], #} &, #], First[#] <= i &, Last /@ # &],
{i, Length[#] - 1}] &;
f8 = Rest@NestList[{Join[#[[1]], {#[[-1, 1]]}], #[[-1, 2 ;;]]} &, {{}, #}, Length@# - 1] &;
f9 = Module[{lst = #},
Function[k, Module[{t = 0}, Split[lst, ++t <= k || (t = -Length@lst) &]]] /@
Range[0, Length[lst] - 2]] &;
f10 = ReplaceList[#, {x__, y__} -> {{x}, {y}}] &; (* one word ? *)
☺ = ♯♯ (♯ = 1; {♯♯[[;; ♯]], ♯♯[[++♯ ;;]]} & /@ {##2 & @@♯♯}); (* no words:)*)
and, for formatting the outputs of the functions above
format = Column[Row /@ #] &;
Examples:
f1 @ Li // format

Equal @@ Through[{f1, f2, f3, f4, f5, f6, f7, f8, f9, f10, ☺} @Range[4]]
True
f1 @ {a,b,a,c,d,b} // format

Equal @@ Through[{f1, f2, f3, f4, f5, f6, f7, f8, f9, f10, ☺} @ {a,b,a,c,d,b}]
True
Notes: I learned about the Or trick in f9 from this answer by Mr.Wizard. See also this answer by Simon Woods.





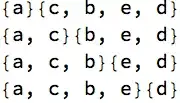




splits[list_] := Table[{Take[list, n], Drop[list, n]}, {n, Length[list] - 1}]– Marius Ladegård Meyer Jul 15 '17 at 11:16