Adjusting Mark McClure's ComplexTicks function in Stan Wagon's book

Question

I'm starting to read chapter 11 of Stan Wagon's third edition of Mathematica in Action, a section written by Mark McClure (and there is a package for the notebook).

I start with:

f[z_] := z^2;
Subscript[z, 0] = 0.9 + 0.15 I;
orbit = NestList[f, Subscript[z, 0], 10]

Then:

Attributes[ComplexTicks] = Listable;
ComplexTicks[s_?NumericQ] := {s, s I} /. 
  Thread[{-1. I, 0. I, 1. I} -> {-I, 0, I}]

What this does, I believe, is create a list of tick marks drawn with the specified labels. For example:

ComplexTicks[Range[0, .4, 0.1]]

Produces:

{{0., 0}, {0.1, 0. + 0.1 I}, {0.2, 0. + 0.2 I}, {0.3, 0. + 0.3 I}, {0.4, 0. + 0.4 I}}

So, for example, at 0.0 we'll mark with 0; at 0.1 we'll mark with 0.+0.1I; etc. Now, his next code is:

ListPlot[{Re[#], Im[#]} & /@ orbit, Frame -> True,
 FrameTicks -> {Automatic, ComplexTicks[Range[0, 0.4, 0.1]], None, 
   None}]

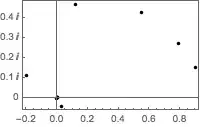
Which is supposed to produce this image:

But that was in an older version of Mathematica. In Mathematica 11.1.1, it produces this image.

The current way to set FrameTicks in Mathematica is FrameTicks->{{left, right},{bottom, top}}. So I adjusted the code as follows:

ListPlot[{Re[#], Im[#]} & /@ orbit, Frame -> True,
 FrameTicks -> {{ComplexTicks[Range[0, 0.4, 0.1]], None}, {Automatic, 
    None}}]

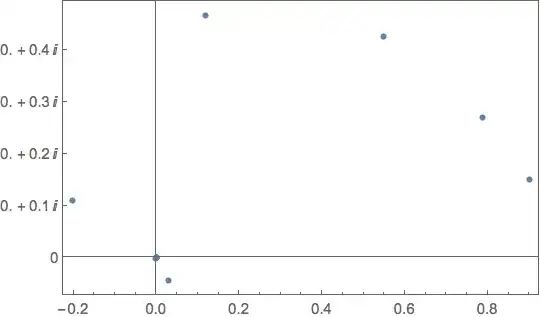
But that gives this image:

Any way to turn off the real zeros in each complex tick number?

Update: Thanks to the help from my colleagues, I gave this a try.

Attributes[ComplexTicks] = Listable;

ComplexTicks[s_?NumericQ] := {s, s "\[ImaginaryI]"} /. 
  Thread[{-1. "\[ImaginaryI]", 0. "\[ImaginaryI]", 
     1. "\[ImaginaryI]"} -> {-I, 0, I}]

f[z_] := z^2;
z0 = 0.9 + 0.15 I;
orbit = NestList[f, z0, 10];

ListPlot[{Re[#], Im[#]} & /@ orbit, Frame -> True,
 FrameTicks -> {{ComplexTicks[Range[0, 0.4, 0.1]], None}, {Automatic, 
    None}}]

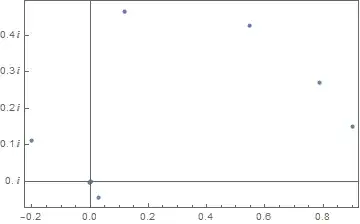
The resulting image is next:

Any thoughts?

Related: Chopping matrix elements, real or imaginary. – MarcoB Jul 17 '17 at 18:25 — MarcoB, Jul 17 '17 at 18:25

score 4 · Answer 1 · answered Jul 17 '17 at 18:31

4

At some point, Mathematica started showing the real part in inexact complex numbers. To workaround this, I would change ComplexTicks to something like:

ComplexTicks[s_?NumericQ] := {s, s Defer[I]}

or

ComplexTicks[s_?NumericQ] := {s, s HoldForm[I]}

answered Jul 17 '17 at 18:31

Carl Woll

130,679
6
243
355

1

Or: ComplexTicks[s_?NumericQ] := {s, s "\[ImaginaryI]"}. – Jens Jul 17 '17 at 19:31

score 0 · Answer 2 · answered Jul 17 '17 at 18:38

0

If it's just a visualization requirement, perhaps you could use:

ComplexTicks[s_?NumericQ] := {s, ToString[s] <> ToString[" \[ImaginaryI]"]}

Mathematica graphics

answered Jul 17 '17 at 18:38

MarcoB

67,153
18
91
189

That would produce some pretty horrifying output for ComplexTicks[10^-1] or ComplexTicks[.000001]. – Carl Woll Jul 17 '17 at 18:41
@CarlWoll Yep, you're right, it would. – MarcoB Jul 17 '17 at 19:33

Adjusting Mark McClure's ComplexTicks function in Stan Wagon's book

2 Answers2