How to numerically solve this non-linear ODE with initial guess function

Question

I have the following non-linear differential equation:

{r t''[r] + t'[r] - 1/r Sin[t[r]] Cos[t[r]] + (4 k)/\[Pi] Sin[t[r]]^2 
 - h r Sin[t[r]] - r Sin[t[r]] Cos[t[r]] == 0, 
 t[0] == \[Pi], t[Infinity] == 0}

with parameters k and h. Let's say for now k=2/3 and h=0. I know that the solution can be well approximated by

t0[r_, r0_] := 2 Pi - 2 ArcTan[Exp[(r - r0)]] - 2 ArcTan[Exp[(r + r0)]]

with some positive r0 on the order of 1. The function looks like this:

Also, one can probably replace the Infinity in the boundary conditions by some value >10.

How can I use this knowledge to (numerically) solve the DE?

So far, I tried replacing Infinity by 20 and using NDSolve with various simple (simple as in not requiring additional parameters) Methods. Sometimes I get a result, but they always look wrong, like this one:

I believe that the key here is to somehow use my knowledge of the approximate solution.

Answer 1

Problems like this usually are challenging, because they involve integrating along the separatrix of a nonlinear ODE, and doing so is numerically unstable. Therefore, no matter how well the initial conditions are chosen, the integration eventually will depart from the desired result. Nonetheless, integration over a reasonable distance certainly is possible. For instance, with the parameters given in the question,

r0 = 10^-2; rmax = 10;
s = NDSolveValue[{r t''[r] + t'[r] - 1/r Sin[t[r]] Cos[t[r]] + (4 k)/π Sin[t[r]]^2 - 
    h r Sin[t[r]] - r Sin[t[r]] Cos[t[r]] == 0, t[r0] == π, 
    t[rmax] == 0} /. h -> 0 /. k -> 2/3, t, {r, r0, rmax}]
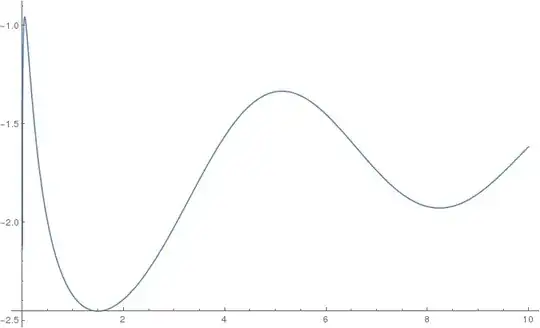
Plot[s[r], {r, r0, rmax}, PlotRange -> All, ImageSize -> Large, 
    LabelStyle -> Directive[12, Bold, Black]]

However, integrating to r = 15 or so will show instability. Furthermore, other parameters may show other instability behavior, so some experimentation may be required. More powerful, but also more burdensome, approaches are available, if needed.

Addendum - Improved Boundary Condition

It often is helpful to solve the linearized ODE at large r.

(Series[(r t''[r] + t'[r] - 1/r Sin[t[r]] Cos[t[r]] + (4 k)/\[Pi] Sin[t[r]]^2 - 
    h r Sin[t[r]] - r Sin[t[r]] Cos[t[r]])/r, {t[r], 0, 1}] // Normal) == 0
Flatten@DSolve[%, t[r], r, Assumptions -> r > 0];
cf[e_]:= 100 Count[e, _BesselJ, Infinity] + 100 Count[e, _BesselY, Infinity] + LeafCount[e]
FullSimplify[% /. C[2] -> I Pi C[2]/2 /. C[1] -> C[1] - Pi C[2]/2 /. C[1] -> I C[1], 
    r > 0, ComplexityFunction -> cf]
(* (-1 - h - 1/r^2) t[r] + t'[r]/r + t''[r] == 0 *)
(* {t[r] -> BesselI[1, Sqrt[1 + h] r] C[1] + BesselK[1, Sqrt[1 + h] r] C[2]} *)

(The last two lines are needed to obtain an explicitly real solution.) That the asymptotic solution contains BesselI is another indication that infinitesimal errors in numerical integration can cause the solution to diverge from the separatrix. The asymptotic solution also can be used to obtain a more accurate boundary condition at large r.

asym = t[r] /. % /. C[1] -> 0;
bc = t'[r]/t[r] == D[asym, r]/asym /. r -> rmax
(* t'[rmax]/t[rmax] == (Sqrt[1 + h] (-BesselK[0, Sqrt[1 + h] rmax] - 
   BesselK[2, Sqrt[1 + h] rmax]))/(2 BesselK[1, Sqrt[1 + h] rmax]) *)

Using bc instead of t[rmax] == 0 often permits good accuracy with smaller values of rmax.