4

I'm trying to use Mathematica to get some early approximate solutions to a system of algebraic and partial differential equations. It is actually 1D model of an ideal gas in a tube. I'll divide my question into two parts so it will be more understandable:

  • Part one:

I want to solve Navier–Stokes equations for a compressible inviscid isothermal fluid in a 1D tube:

  1. $\frac{\partial P}{\partial t}+\frac{\partial \left( \nu P \right)}{\partial u}=0$

  2. $\frac{\partial \left(P \nu\right) }{\partial t}+\frac{\partial \left( P \nu^2 \right) }{\partial u}+\mathring{R} T_a\frac{\partial P}{\partial u}=0$

Initial condition:

  1. $\nu\left( u,0 \right)=0$
  2. $P\left( u,0 \right)=1$

Dirichlet boundary condition (step signal)

$\left\{\begin{matrix} if \, t<1 \, then & \nu\left( 0,t \right)=0 \\ else & P\left( 0,t \right)=2 \end{matrix}\right.$

and $P\left( 1,t \right)=1$

I know I can use NDSolveValue and NDSolve to have some numerical solutions. for example I used the command below to solve a simplified version of the above system of PDEs:

pval = NDSolveValue[{D[p[x, t]*v[x, t], x] + D[p[x, t], t] == 0, 
D[p[x, t], x] + D[p[x, t]*v[x, t]^2, x] + D[p[x, t]*v[x, t], t] == 
0, p[0, t] == UnitStep[t - 1] + 1, p[1, t] == 1, p[x, 0] == 1, 
v[x, 0] == 0}, p, {x, 0, 1}, {t, 0, 3}, 
Method -> {"MethodOfLines", "TemporalVariable" -> t, 
"SpatialDiscretization" -> {"TensorProductGrid", 
  "MaxPoints" -> 4000, "MinPoints" -> 4000}}, MaxStepSize -> 0.001]
Dimensions[sol1["Grid"]]

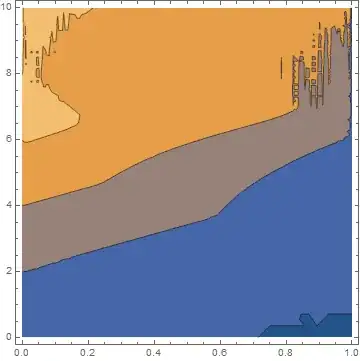
but the result I get is pretty awful:

ContourPlot[pval[x, t], {x, 0, 1}, {t, 0, 2.2}]

enter image description here

and it does not go furthure than t=2.232...

My first guess I don't have the right temporal resolution, but I don't know how to set it like what I have found for spatial resolution.

But I would like to ask my question in a general form:

  1. How should I solve this system of algebraic and PDEs. DSolve, NDSolveValue or NDSolve?

  2. how to get reasonable solutions by setting the spatial and temporal step size?

    • Part two:

I would like to solve the Navier–Stokes equations for a compressible viscose adiabatic fluid in a 1D tube:

  1. Ideal gas: $P=\mathring{R} T \rho$
  2. conservation of mass: $\frac{\partial \rho}{\partial t}+\frac{\partial \left( \nu \rho \right)}{\partial u}=0$
  3. conservation of linear momentum: $\frac{\partial \left(\rho \nu\right) }{\partial t}+\frac{\partial \left( \rho \nu^2 \right) }{\partial u}+\frac{\partial P}{\partial u}-\frac{4\mu\nu}{D}=0$
  4. conservation of heat for a control volume, assuming the Newtonian viscose fluid, the conduction/radiation is negligible (adiabatic for the whole tube): $\mu\nu^2=\frac{cD}{4}\left( \frac{\partial\left( T\rho\nu \right)}{\partial u}+\frac{\partial \left(\rho T \right)}{\partial t} \right)$

these equations in Mathematica format: 

p[x, t] == T[x, t]*q[x, t]
D[q[x, t]*v[x, t], x] + D[q[x, t], t] == 0
D[p[x, t], x] + D[q[x, t]*v[x, t]^2, x] + D[q[x, t]*v[x, t], t] -v[x,t]==0
v[x, t]^2 - D[T[x, t]*q[x, t]*v[x, t], x] == 0

Where $\mathring{R}$, $\nu$, $D$ and $c$ are constants. $P$, $\rho$, $\nu$ and $T$ are functions of $x$ and $t$

I would like to ask my question in a general form:

  1. How should I solve this system of algebraic and PDEs. DSolve, NDSolveValue or NDSolve?
  2. how to get reasonable solutions by setting the spatial and temporal step size?

P.S. I'm not able to get the right tags for my post!

bbgodfrey
  • 61,439
  • 17
  • 89
  • 156
Foad
  • 605
  • 4
  • 13
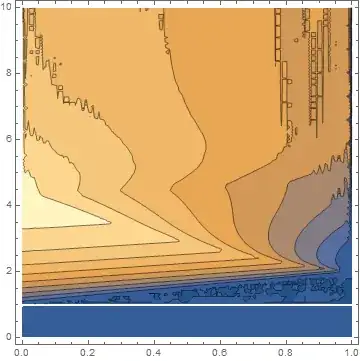
  • NDSolve and NDSolveValue in general produce the same result,. DSolve is unlikely to produce a solution for this nonlinear problem. Your plot suggests that the solution may be unstable numerically for the parameters chosen. – bbgodfrey Jul 31 '17 at 14:01
  • @bbgodfrey you are right, there were some mistakes. I also updated the code and the picture – Foad Jul 31 '17 at 14:26
  • With MaxStepSize -> {10^-3, 2 10^-4}], the computation goes beyond 2.23 without difficulty, although it does show signs of numerical instability beyond t == 5. What, precisely, is your question? – bbgodfrey Jul 31 '17 at 14:35
  • I would like to solve the system of PDEs I mentioned. That's the main question. – Foad Jul 31 '17 at 14:37
  • Well, if you can help me with the complete version it would be the best. I think I kind of made mistake adding the simplified version to this question. sorry for that. I just added the Mathemathica code to the question – Foad Jul 31 '17 at 14:46
  • @bbgodfrey first of all thanks a lot for being patient and answering my question. I still don't have the upvote privilege otherwise I would do that. secondly. I spent sometime cleaning the question and making it more structured. – Foad Aug 01 '17 at 02:22
  • 1
    p[0, t] == UnitStep[t - 1] + 1 does not accurately represent your x == 0 boundary condition. Also, you may wish to delete some of the old material now at the end of your question. Best wishes. – bbgodfrey Aug 01 '17 at 04:16
  • @bbgodfrey 1. you are right about the boundary condition. but I still don't know how to include that discrete "if-statement" as a boundary condition 2. There is a lot for me to learn about NDSolve. I'm going to spend some time learning and adding them to your answer or a new one. 3. I'm thinking of moving the second part to a new question maybe. it is too long. 4. "the end of your question" do you mean the P.S. about tags? I still think there aren't enough tags. for example NDSolve should be a tag, PDE should also be one. – Foad Aug 01 '17 at 08:27
  • Probably, it is necessary to discretize by hand the PDE into a set of ODEs to accommodate the boundary condition. 2) Visit here to learn much more about NDSolve. 3) Focus on the simple question first. 4) I recommend against creating new tags, which only causes confusion; the ones I added should be sufficient. 5) Delete comments that no longer are relevant.
    • – bbgodfrey Aug 01 '17 at 16:09
  • As pointed out by @bbgodfrey, your question seems to be similar to the one linked below. If they're really the same type of question, then your b.c. is mistakenly given. If they're not, your b.c. still looks suspicious: there's no b.c. for $\nu$ when $t>1$? – xzczd Aug 01 '17 at 17:32
  • @xzczd honestly I was too hasty posting the question. it is too big and confusing. I need to spend some time, pinpointing individual issues and then come back and divide the question into multiple ones. about the boundary condition. it is actually a valve at u=0. so when it opens the pressure is the reservoir pressure and when it closes, the velocity is zero. is it a problem? – Foad Aug 01 '17 at 23:27
  • I'm not sure I should say. As mentioned above, I just feel it suspicious, there does exist some special cases (for example this), but usually b.c. for $\nu$ is needed for all time. – xzczd Aug 02 '17 at 04:32