Solve an ODE using matrices

Question

I have the following system: $m\cdot\frac{dx^2}{dt^2}=-k(x-lo)-\frac{dx}{dt}\cdot d+m\cdot g$ It represents a mass with a spring and a damper. It is easy to solve using NDSolve but I'm trying to solve it using matrices. (Because if we represent the system using state equations, we can use some transformations, like diagonalization or triangularization so the time of computation is reduced). I tried using regular matrices but it doesn't work. Is there any way to do this? The system after an order reduction is:

$ \begin{bmatrix} x1'(t) \\ x2'(t) \\ \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ \frac{-k}{m} & \frac{-d}{m} \\ \end{bmatrix} \begin{bmatrix} x1 \\ x2 \\ \end{bmatrix}+ \begin{bmatrix} 0\\ \frac{1}{m}\\ \end{bmatrix} f(t) + \begin{bmatrix} 0\\ \frac{kl_o}{m}+g\\ \end{bmatrix} $

where $f(t)=15u(t-5)$ (u(t) is the unit step function).

I have tried this:

lo = 0.50; m = 1.5; k = 20; d = 3; g = 9.8;
A = {{0, 1}, {-k/m, -m}}  
z[t_] = 15*HeavisideTheta[t - 5];
b = {{0}, {1/m}};
γ = {{0}, {(k*lo)/m + g}};
S = A*{{x0[t]}, {x1[t]}} + b*z[t] + γ 
eqns = {{x0'[t]}, {x1'[t]}} 
NDSolve[{eqns == A*{{x0[t]}, {x1[t]}} + b*z[t] + γ , 
  x0[0] == 0, x1[0] == 0}, {x0[t], x1[t]}, {t, 0, 10}]

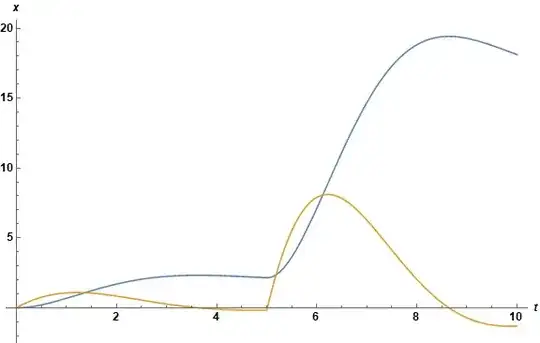
As a tip: HeavisideTheta[] is intended for symbolic use only; for numerics, like in your situation, please use UnitStep[]. Also, matrix-vector multiplication is . (Dot[]), not * (Times[]). — J. M.'s missing motivation, Aug 03 '17 at 01:47
Thanks! Now it works better. I tried to solve the system with f(t)=0 and I got the correct solution using your tips. But I still can't get the solution using f(t). (Mathematica says "non-numerical value at t==0" ) — Miguel Duran Diaz, Aug 03 '17 at 02:31
Please include such constants in your questions the next time instead of making other people ask for them. — J. M.'s missing motivation, Aug 03 '17 at 02:56

score 3 · Accepted Answer · answered Aug 03 '17 at 02:34

3

The code runs with a few minor modifications, as suggested by J.M. In addition, A was corrected, and constants given numerical values. Then,

k = 1; lo = 1; m = 1; d = 1; g = 1;
A = {{0, 1}, {-k/m, -d/m}};
z[t_] = 15*UnitStep[t - 5];
b = {{0}, {1/m}};
γ = {{0}, {(k*lo)/m + g}};
eqns = {{x0'[t]}, {x1'[t]}};
s = Flatten@NDSolve[{eqns == A.{{x0[t]}, {x1[t]}} + b z[t] + γ, 
    x0[0] == 0, x1[0] == 0}, {x0[t], x1[t]}, {t, 0, 10}]

answered Aug 03 '17 at 02:34

bbgodfrey

61,439
17
89
156

I know the basic use of Flatten, but you used here to solve the system. Why does it work with Flatten, but it didn't work using regular matrix operations? I mean, why is it necessary to use Flatten? – Miguel Duran Diaz Aug 03 '17 at 02:46
1

@MiguelDuranDiaz Flatten is used only to remove an extra set of { } from s for plotting purposes. It has nothing to do with obtaining a solution. – bbgodfrey Aug 03 '17 at 02:50
@Miguel, if you'd used vectors instead of column matrices, then the Flatten[] would not have been necessary, as Carl notes: With[{lo = 0.50, m = 1.5, k = 20, d = 3, g = 9.8}, NDSolveValue[{{x0'[t], x1'[t]} == {{0, 1}, {-k/m, -d/m}}.{x0[t], x1[t]} + {0, 1/m} (15 UnitStep[t - 5]) + {0, k lo/m + g}, x0[0] == 0, x1[0] == 0}, {x0, x1}, {t, 0, 10}]]. Please see this. – J. M.'s missing motivation Aug 03 '17 at 03:04

Carl Woll · Answer 2 · 2017-08-03T02:44:22.620

I would avoid column matrices:

A = {{0,1},{-k/m,-d/m}};
z[t_]:={0, 15UnitStep[t-5]}
lo = 0.50; 
m = 1.5; 
k = 20; 
d = 3; 
g = 9.8;
b = {0,1/m};
γ = {0,(k lo)/m+g};

Then, you can use the vector form of NDSolve/NDSolveValue as follows:

sol = NDSolveValue[
    {x'[t] == A . x[t] + b z[t] + γ, x[0] == {0,0}},
    x,
    {t,0,10}
]

InterpolatingFunction[{{0., 10.}}, <>]

Finally, a plot:

Plot[sol[t], {t, 0, 10}]

Solve an ODE using matrices

2 Answers2