How to overlap ContourPlots

Question

I have the following functions, which are

x^2 - y^2

and

2 x y

of two variables which represent the real and imaginary part of a complex function $f(z)$. I want to show that the contour lines of the two function intersect perpendicularly. I have the two ContourPlot

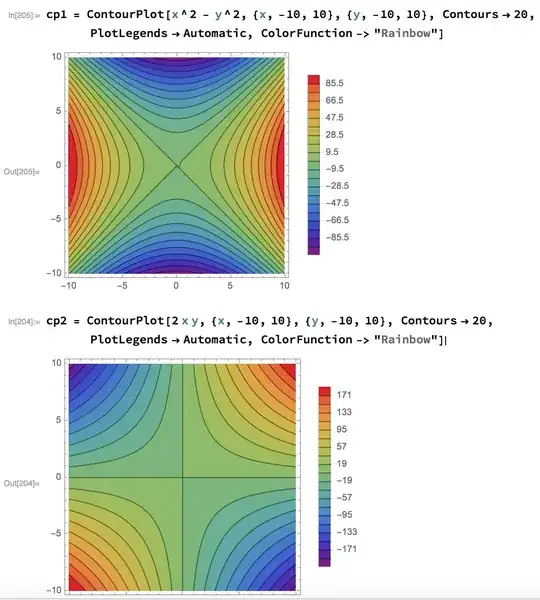
cp1 = ContourPlot[x^2 - y^2, {x, -10, 10}, {y, -10, 10}, 
   Contours -> 20,
    PlotLegends -> Automatic, ColorFunction -> "Rainbow"];
cp2 = ContourPlot[2 x y, {x, -10, 10}, {y, -10, 10}, Contours -> 20,
    PlotLegends -> Automatic, ColorFunction -> "Rainbow"];

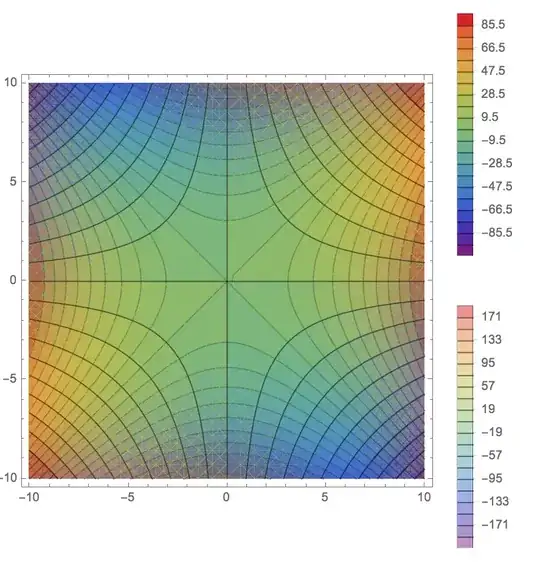
What I would like to do is to overlap the two plots keeping the color between the contour lines, but with opacity so that I can see the contours below intersecting normally the contours above.

I partially achieved this result with:

cp1 = ContourPlot[x^2 - y^2, {x, -10, 10}, {y, -10, 10}, 
   Contours -> 20,
    PlotLegends -> Automatic, ColorFunction -> "Rainbow"];
cp2 = ContourPlot[2 x y, {x, -10, 10}, {y, -10, 10}, 
    Mesh -> None, 
    (*ContourShading->None, *)

   ColorFunction -> Function[f, Opacity[.5, ColorData["Rainbow"][f]]], 
    Contours -> 20,
    PlotLegends -> Automatic
    ];
Show[cp1, cp2]

but as you can notice there's a strange grid below the fist plot...

EDIT (completness):

I'm using mathematica 11.1.0.0

No strange grid for me. I'm using version 11.1. What are you using? — Hugh, Aug 06 '17 at 19:12
Related: https://mathematica.stackexchange.com/questions/2629/avoiding-white-lines-inside-filled-area-in-regionplot-exported-as-pdf-or-ps/2630#2630 — Michael E2, Aug 06 '17 at 19:22
Try ContourPlot[ReIm[(x + I y)^2], {x, -5, 5}, {y, -5, 5}, ContourShading -> None, ContourStyle -> {ColorData[97, 1], ColorData[97, 2]}] — J. M.'s missing motivation, Aug 06 '17 at 19:24
Adding Style[Show[cp1, cp2], Antialiasing -> False] Following the link for Michael E2 may work. — Hugh, Aug 06 '17 at 19:27
@J.M. this will plot only the lines, that is not what I really whished... — opisthofulax, Aug 06 '17 at 19:29
@Hugh even with the anti-aliasing I still have the grid, plus it has very bad resolution... — opisthofulax, Aug 06 '17 at 19:30
I can reproduce it on V11.1.1 (Mac). -- I'm more interested in what sort of background you really want. I don't see why blending the two (opacity = 50%) is worth it. — Michael E2, Aug 06 '17 at 19:31
I understand, on Grapher, if you overlap the two colorised level set you obtain a fancy effect which help you visualise the growing rate or the decay... I was hoping there was something similar on Mathematica. — opisthofulax, Aug 06 '17 at 19:33
Do you still get the same effect if you modify the second ColorFunction to ColorFunction -> Function[f, Append[ColorData["Rainbow", f], 0.5]]? — J. M.'s missing motivation, Aug 06 '17 at 19:33
Yes, still there... I can't understand why it works for you but not for me... doesn't it sound strange? — opisthofulax, Aug 06 '17 at 19:35
This works for me: Show[cp1, cp2 /. EdgeForm[] -> EdgeForm[Directive[Opacity[0]]]]. Does it for you? — Michael E2, Aug 06 '17 at 19:38
That's the reason for asking for your OS; I don't see this on Linux. — J. M.'s missing motivation, Aug 06 '17 at 19:38
Darn! There are faint edge lines from the underlying plot...I can't hardly see them and missed them until I exported to PNG. — Michael E2, Aug 06 '17 at 19:45
@MichaelE2 wow that worked for me, thanks a lot... what was the problem due to? If you make a complete answer I'l give you the correct one ;) Thanks again anyway — opisthofulax, Aug 06 '17 at 20:03
Ok, no, I didn't zoomed... there are still the grid lines, but now are very thin, so the outcome is acceptable for me, even if it would be good not to have them at all — opisthofulax, Aug 06 '17 at 20:05
I posted an answer, but maybe someone will fix cp1. (The same trick does not work on it.) — Michael E2, Aug 06 '17 at 20:10
The option Exclusions -> {x^2 + y^2 == 0.0001} also fixes the kink at the origin in cp1. — Michael E2, Aug 06 '17 at 20:25

score 3 · Accepted Answer · answered Aug 06 '17 at 20:09

3

Try

Show[cp1, cp2 /. EdgeForm[] -> EdgeForm[Opacity[0]]]

Mathematica graphics

The lines in the OP come from the edges of the polygons forming the contour shading. The above trick makes them invisible.

(The OP said this is acceptable, but I see faint, dark lines from the edges of the polygons of cp1.)

answered Aug 06 '17 at 20:09

Michael E2

235,386
17
334
747

1

@opisthofulax Try adding the option MaxRecursion -> 3 to the ContourPlot[] for cp1. Stationary points are singular points for ContourPlot, in that the contour through one is usually not a single, simple curve. Normally you can't fix it, but you can make it smaller. Increasing PlotPoints and/or MaxRecursion is how you do might that. – Michael E2 Aug 06 '17 at 20:20
1

Exclusions -> {x^2 + y^2 == 0.0001} also works. – Michael E2 Aug 06 '17 at 20:25

How to overlap ContourPlots

EDIT (completness):

1 Answers1